
分析 (1)將兩女生看作一個元素,使用捆綁法排列;
(2)插空法排列;
(3)相除法計算;
(4)分類法計算.
解答 解:(1)兩名女生站在一起有站法A${\;}_{2}^{2}$種,視為一種元素與其余5人全排,有A${\;}_{6}^{6}$種排法.
故有不同站法A${\;}_{2}^{2}$•A${\;}_{6}^{6}$=1 440種.
(2)先站老師和女生,有站法A${\;}_{3}^{3}$種,再在老師和女生站位的間隔(含兩端)處插入男生,每空一人,有插入方法A${\;}_{4}^{4}$種.
故共A${\;}_{3}^{3}$•A${\;}_{4}^{4}$=144種.
(3)7人全排列中,4名男生不考慮身高順序的站法有A${\;}_{4}^{4}$種,而由高到低有從左到右,或從右到左的不同.
故共有不同站法2•$\frac{{A}_{7}^{7}}{{A}_{4}^{4}}$=420種.
(4)中間和兩端是特殊位置,可如下分類求解:
①老師站兩端之一,另一端由男生站,有A${\;}_{2}^{1}$•A${\;}_{4}^{1}$•A${\;}_{5}^{5}$種站法,
②兩端全由男生站,老師站除兩端和正中間的另外4個位置之一,有A${\;}_{4}^{2}$•A${\;}_{4}^{1}$•A${\;}_{4}^{4}$種站法.
故共有不同站法有A${\;}_{2}^{1}$•A${\;}_{4}^{1}$•A${\;}_{5}^{5}$+A${\;}_{4}^{2}$•A${\;}_{4}^{1}$•A${\;}_{4}^{4}$=2 112種.
點評 本題考查了計數原理,排列與排列數的計算,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$ | B. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{1}{3}$$\overrightarrow{CD}$ | C. | $\overrightarrow{EF}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{2}{3}$$\overrightarrow{CD}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
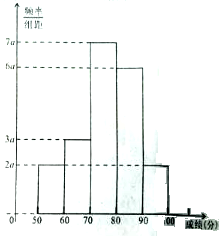 20名學生某次數學考試成績(單位:分)的頻率分布直方圖如圖.
20名學生某次數學考試成績(單位:分)的頻率分布直方圖如圖.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com