
分析 根據題意求出|$\overrightarrow{a}$+$\overrightarrow{b}$|的值,求出向量($\overrightarrow{a}$+$\overrightarrow{b}$)與$\overrightarrow{a}$的夾角為θ的余弦值,再利用數量積公式和向量投影的定義,即可求出向量$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影值.
解答 解:$|\overrightarrow a|=1$,$|\overrightarrow b|=2$,$\overrightarrow a$與$\overrightarrow b$的夾角為60°,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|×|$\overrightarrow{b}$|×cos60°=1×2×$\frac{1}{2}$=1;
由此可得($\overrightarrow{a}$+$\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+2$\overrightarrow{a}$•$\overrightarrow{b}$+|$\overrightarrow{b}$|2=1+2+4=7,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$;
設$\overrightarrow{a}$+$\overrightarrow{b}$與$\overrightarrow{a}$的夾角為θ,
∵($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=|$\overrightarrow{a}$|2+$\overrightarrow{a}$•$\overrightarrow{b}$=1+1=2,
∴cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+\overrightarrow{b}|×|\overrightarrow{a}|}$=$\frac{2}{\sqrt{7}×1}$=$\frac{2\sqrt{7}}{7}$,
可得向量$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影為:
|$\overrightarrow{a}$+$\overrightarrow{b}$|cosθ=$\sqrt{7}$×$\frac{2\sqrt{7}}{7}$=2.
故答案為:2.
點評 本題考查了平面向量數量積的定義、向量的夾角公式以及模長、投影的概念與計算問題,屬于基礎題目.


 教學練新同步練習系列答案
教學練新同步練習系列答案科目:高中數學 來源: 題型:選擇題
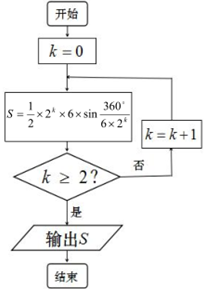 公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近于圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的(四舍五入精確到小數點后兩位)的值為( )(參考數據:sin15°=0.2588,sin75°=0.1305)
公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近于圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的(四舍五入精確到小數點后兩位)的值為( )(參考數據:sin15°=0.2588,sin75°=0.1305)| A. | 3.10 | B. | 3.11 | C. | 3.12 | D. | 3.13 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -4 | C. | -3 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com