
分析 (1)求出函數的導數,解關于導函數的方程,求出函數的單調區間,得到函數的極值即可;
(2)求出函數h(x)的導數,通過討論a的范圍,求出函數的單調區間,得到函數的極值點,求出m的范圍即可.
解答 解:(1)f(x)的定義域是(0,+∞),
令f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$=0,解得:x=1,
x∈(0,1)時,f′(x)<0,f(x)遞減,
x∈(1,+∞)時,f(x)遞增,
∴f(x)在x=1處取得極小值,且極小值f(1)=2,無極大值,
令g′(x)=1-$\frac{1}{{x}^{2}}$=0,解得:x=1(x=-1舍去),
∴當x∈(0,1)時,g′(x)<0,g(x)遞減,
當x∈(1,+∞)時,g′(x)>0,g(x)遞增,
∴g(x)在x=1處取得極小值,且極小值g(1)=2,無極大值,
故兩個函數有相同的極小值點x=1,且所求的極小值是2;
(2)h(x)=f(x)-ag(x)=lnx+$\frac{1}{x}$+1-ax-$\frac{a}{x}$,其定義域是(0,+∞),
則h′(x)=$\frac{-(x-1)(ax+a-1)}{{x}^{2}}$,
a=0時,h′(x)=0僅有1個解,x=1不合題意,
當a≠0時,令h′(x)=0,解得:x=1或x=$\frac{1-a}{a}$,
由題意得:$\frac{1-a}{a}$>0,且$\frac{1-a}{a}$≠1,∴a∈(0,$\frac{1}{2}$)∪($\frac{1}{2}$,1),
此時,h(x)的兩個極值點分別是x=1和x=$\frac{1-a}{a}$,
當a∈(0,$\frac{1}{2}$)時,$\frac{1-a}{a}$>1,∴x1=1,x2=$\frac{1-a}{a}$,h(x1)=h(1)=2-2a,
而當2-2a∈(1,2),又h(x1)<m恒成立,則m≥2,
當a∈($\frac{1}{2}$,1)時,$\frac{1-a}{a}$<1,∴x1=$\frac{1-a}{a}$,x2=1,
h(x1)=h($\frac{1-a}{a}$)=ln$\frac{1-a}{a}$+2a,
設ω(a)=ln$\frac{1-a}{a}$+2a,則ω′(a)=-$\frac{{2(a-\frac{1}{2})}^{2}+\frac{1}{2}}{a(1-a)}$<0,
∴ω(a)在($\frac{1}{2}$,1)上是減函數,ω(a)<ω($\frac{1}{2}$)=1,
∴h(x1)=ln$\frac{1-a}{a}$+2a<1,
又h(x1)<m恒成立,則m≥1,
綜上,實數m的范圍是[2,+∞).
點評 本題考查了函數的單調性、極值問題,考查導數的應用以及分類討論思想,轉化思想,是一道綜合題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
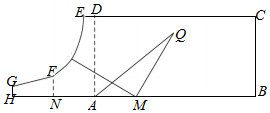 如圖,某地區有一塊長方形植物園ABCD,AB=8(百米),BC=4(百米),植物園西側有一塊荒地,現計劃利用該荒地擴大植物園面積,使得新的植物園為HBCEFG滿足下列要求:E在CD的延長線上,H在BA的延長線上,DE=0.5(百米),AH=4(百米),N為AH的中點,FN⊥AH,EF為曲線段,它上面的任意一點到AD與AH的距離乘積為定值,FG,GH均為線段,GH⊥HA,GH=0.5(百米).
如圖,某地區有一塊長方形植物園ABCD,AB=8(百米),BC=4(百米),植物園西側有一塊荒地,現計劃利用該荒地擴大植物園面積,使得新的植物園為HBCEFG滿足下列要求:E在CD的延長線上,H在BA的延長線上,DE=0.5(百米),AH=4(百米),N為AH的中點,FN⊥AH,EF為曲線段,它上面的任意一點到AD與AH的距離乘積為定值,FG,GH均為線段,GH⊥HA,GH=0.5(百米).查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知球內接正四棱錐P-ABCD的高為3,AC,BC相交于O,球的表面積為$\frac{169π}{9}$,若E為PC中點.
已知球內接正四棱錐P-ABCD的高為3,AC,BC相交于O,球的表面積為$\frac{169π}{9}$,若E為PC中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{12}$h | B. | $\frac{3}{4}$h | C. | $\frac{1}{2}$h | D. | h |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖多面體ABCD中,面ABCD為正方形,棱長AB=2,AE=3,DE=$\sqrt{5}$,二面角E-AD-C的余弦值為$\frac{{\sqrt{5}}}{5}$,且EF∥BD.
如圖多面體ABCD中,面ABCD為正方形,棱長AB=2,AE=3,DE=$\sqrt{5}$,二面角E-AD-C的余弦值為$\frac{{\sqrt{5}}}{5}$,且EF∥BD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com