
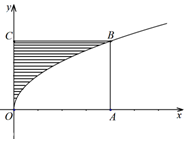
 如圖,長方形OABC中,O為坐標原點,點C在y軸上,A(4,0),曲線y2=ax(a>0)經過點B,現將一質點隨機投入長方形OABC中,若質點落在圖中陰影區域的概率是( )
如圖,長方形OABC中,O為坐標原點,點C在y軸上,A(4,0),曲線y2=ax(a>0)經過點B,現將一質點隨機投入長方形OABC中,若質點落在圖中陰影區域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 首先利用定積分求出陰影部分的面積,然后利用幾何概型的概率公式求解.
解答 解:由題意,陰影部分的面積為${∫}_{0}^{2\sqrt{a}}\frac{{y}^{2}}{a}dy=\frac{1}{3a}{y}^{3}{|}_{0}^{2\sqrt{a}}=\frac{8\sqrt{a}}{3}$,
由幾何概型的公式得到質點落在圖中陰影區域的概率是$\frac{\frac{8\sqrt{a}}{3}}{4×2\sqrt{a}}=\frac{1}{3}$;
故選C.
點評 本題考查了定積分的運用以及幾何概型的概率求法;正確計算陰影部分 面積是前提,利用幾何概型的公式求概率是關鍵.


 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 已知a>1,?x>0,ax≤1 | B. | $已知0<a<1,?{x_0}<0,{a^{x_0}}≤1$ | ||
| C. | $已知0<a<1,?{x_0}≥0,{a^{x_0}}≤1$ | D. | 已知a>1,?x>0,ax≤1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{8}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{2}$ | D. | $\frac{4}{3}\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
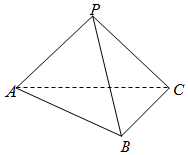 如圖,在三棱錐P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.
如圖,在三棱錐P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com