
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
分析 由題意,本題是幾何概型,首先求出事件對應的區間長度,利用長度比求概率.
解答 解:區間$[{-\frac{5}{6},\frac{13}{6}}]$上隨機取一個數x,對應區間長度為$\frac{13}{6}+\frac{5}{6}=3$,滿足事件“$-1≤{log_{\frac{1}{3}}}({x+1})≤1$”的x范圍為$\frac{1}{3}≤$x+1≤3,即$-\frac{2}{3}$≤x≤2,對應區間長度為2+$\frac{2}{3}=\frac{8}{3}$,
所以事件不發生的概率為1-$\frac{\frac{8}{3}}{3}$=$\frac{1}{9}$;
故選D.
點評 本題考查了幾何概型的概率求法;關鍵是明確幾何測度為區間的長度.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{π-2}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{3π+2}{4π}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=3sin($\frac{π}{6}$-2x) | B. | f(x)=3sin(2x-$\frac{π}{6}$) | C. | f(x)=3sin($\frac{π}{3}$-2x) | D. | f(x)=3sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{5}{3}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | -5 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
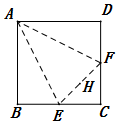 如圖,在正方形ABCD中,E,F分別為BC,CD的中點,H為EF的中點,沿AE,EF,FA將正方形折起,使B,C,D重合于點O,構成四面體,則在四面體A-OEF中,下列說法不正確的序號是②.
如圖,在正方形ABCD中,E,F分別為BC,CD的中點,H為EF的中點,沿AE,EF,FA將正方形折起,使B,C,D重合于點O,構成四面體,則在四面體A-OEF中,下列說法不正確的序號是②.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com