
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根據f(x)為奇函數,設x>0,得-x<0,可求出f(x)=e-x(x-1)判定①正確;
由f(x)解析式求出-1,1,0都是f(x)的零點,判定②錯誤;
由f(x)解析式求出f(x)>0的解集,判斷③正確;
分別對x<0和x>0時的f(x)求導,根據導數符號判斷f(x)的單調性,
根據單調性求f(x)的值域,可得?x1,x2∈R,有|f(x1)-f(x2)|<2,判定④正確.
解答 解:對于①,f(x)為R上的奇函數,設x>0,則-x<0,
∴f(-x)=e-x(-x+1)=-f(x),∴f(x)=e-x(x-1),①正確;
對于②,∵f(-1)=0,f(1)=0,且f(0)=0,
∴f(x)有3個零點,②錯誤;
對于③,x<0時,f(x)=ex(x+1),易得x<-1時,f(x)<0;
x>0時,f(x)=e-x(x-1),易得0<x<1時,f(x)<0;
∴f(x)<0的解集為(-∞,-1)∪(0,1);③正確;
對于④,x<0時,f′(x)=ex(x+2),得
x<-2時,f′(x)<0,-2<x<0時,f′(x)>0;
∴f(x)在(-∞,0)上單調遞減,在(-2,0)上單調遞增;
∴x=-2時,f(x)取最小值-e-2,且x<-2時,f(x)<0;
∴f(x)<f(0)=1;
即-e-2<f(x)<1;
x>0時,f′(x)=e-x(2-x);
∴f(x)在(0,2)上單調遞增,在(2,+∞)上單調遞減;
x=2時,f(x)取最大值e-2,且x>2時,f(x)>0;
∴f(x)>f(0)=-1;
∴-1<f(x)≤e-2;
∴f(x)的值域為(-1,e-2]∪[-e-2,1);
∴?x1,x2∈R,都有|f(x1)-f(x2)|<2;④正確;
綜上,正確的命題是①③④,共3個.
故選:B.
點評 本題考查了奇函數的定義與應用問題,也考查了函數的零點以及不等式的解集、根據導數符號判斷函數單調性和求函數最值、求函數值域的方法,是綜合性題目.


科目:高中數學 來源: 題型:選擇題
| A. | (0.1,0.2,0.3) | B. | (0,0,0.001) | C. | (5,0,0) | D. | (0,0.01,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 28 | C. | 212 | D. | 215 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
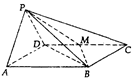 如圖,在四棱錐中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M為CD的中點,平面PAD⊥平面ABCD.
如圖,在四棱錐中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M為CD的中點,平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 3 | B. | 4 | C. | 6 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1+i | B. | 1-i | C. | $\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$ | D. | $\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}i$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com