
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
分析 求函數的導數,分別利用函數單調性和導數之間的關系進行判斷即可.
解答 解:函數的定義域為(0,+∞),
函數的導數f′(x)=$\frac{2k-1}{x}$-$\frac{k}{{x}^{2}}$+2=$\frac{2{x}^{2}+(2k-1)x-k}{{x}^{2}}$=$\frac{(x+k)(2x-1)}{{x}^{2}}$=$\frac{2(x+k)(x-\frac{1}{2})}{{x}^{2}}$,
①當k=-$\frac{1}{2}$時,f′(x)=$\frac{2(x-\frac{1}{2})^{2}}{{x}^{2}}$≥0恒成立,則函數f(x)在(0,+∞)上單調遞增,
則在(0,$\frac{1}{2}}$)上單調遞增,故①正確;
②當k≥0時,由f′(x)>0得x>$\frac{1}{2}$,此時函數為增函數,
由f′(x)<0,得0<x<$\frac{1}{2}$,此時函數為減函數,即當x=$\frac{1}{2}$時,函數f(x)存在極小值,
即可函數f(x)在(0,+∞)上有極大值錯誤,故②錯誤;
③當-$\frac{1}{2}$<k<0時,則0<-k<$\frac{1}{2}$,
由f′(x)<0得-k<x<$\frac{1}{2}$,
由f′(x)>0得0<x<-k或x>$\frac{1}{2}$,即函數f(x)在($\frac{1}{2}$,+∞)上單調遞增;故③錯誤,
④當k<-$\frac{1}{2}$時,-k>$\frac{1}{2}$,由f′(x)>0得0<x<$\frac{1}{2}$或x>-k,此時函數單調遞增,
由f′(x)<0得$\frac{1}{2}$<x<-k,即函數為減函數,
即函數f(x)在(0,+∞)上有極大值f(${\frac{1}{2}}$),有極小值f(-k).故④正確,
故不正確命題的序號②③,
故選:B
點評 本題主要考查命題的真假判斷,涉及函數的單調性和導數的關系,考查學生的計算能力.


科目:高中數學 來源: 題型:選擇題
| A. | 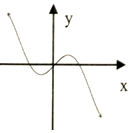 | B. |  | C. | 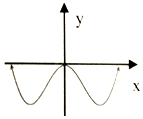 | D. | 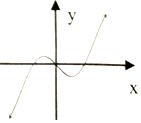 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第二、四象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | am+1<am+2 | B. | am+1>bm+2 | C. | bm+2<am+2 | D. | bm+1>bm+2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com