波多野结衣先锋影音,av在线成人,久久久久一区

19．已知k是正整數，且1≤k≤2017，則滿足方程sin1°+sin2°+…+sink^°=sin1°•sin2°…sink^°的k有11個．

分析由三角函數的值域可知，除k=1外當等式sin1°+sin2°+…+sink^°=sin1°•sin2°…sink^°的左右兩邊均為0時等式成立，由此可得正整數k的個數．

解答解：由三角函數的單調性及值域，可知sin1°•sin2°…sink^°＜1．
∴除k=1外只有當等式sin1°+sin2°+…+sink^°=sin1°•sin2°…sink^°的左右兩邊均為0時等式成立，
則k=1、359、360、719、720、1079、1080、1439、1440、1799、1800時等式成立，
滿足條件的正整數k有11個．
故答案為：11．

點評本題考查三角函數的化簡求值，尋找規律是解答該題的關鍵，是基礎題．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：選擇題

9．已知動點M到點A（2，0）的距離是它到點B（8，0）的距離一半，則動點M的軌跡方程是（　　）

A．

（x-2）²+y²=16

B．

x²+y²=16

C．

（x-4）²+y²=16

D．

x²+y²=4

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

10．已知$sinα+cosα=\frac{1}{5}$，且$-\frac{π}{2}≤α≤\frac{π}{2}$，那么tanα等于（　　）

A．

$-\frac{4}{3}$

B．

$-\frac{3}{4}$

C．

$\frac{3}{4}$

D．

$\frac{4}{3}$

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

7．

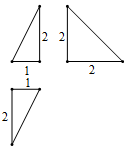已知某三棱錐的三視圖如圖所示，圖中的3個直角三角形的直角邊長度已經標出，則在該三棱錐中，最短的棱和最長的棱所在直線的成角余弦值為（　　）

A．

$\frac{1}{3}$

B．

$\frac{{\sqrt{5}}}{5}$

C．

$\frac{1}{2}$

D．

$\frac{2}{3}$

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

14．

如圖，等腰三角形ABC中，∠B=∠C，D在BC上，∠BAD大小為α，∠CAD大小為β．
（1）若$α=\frac{π}{4}，β=\frac{π}{3}$，求$\frac{BD}{DC}$；
（2）若$\frac{BD}{DC}=\frac{1}{2}，β=α+\frac{π}{3}$，求∠B．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

4．若函數f（x）=a³-cosx，則f'（a）=（　　）

A．

3a²+sina

B．

3a²-sina

C．

sina

D．

cosa

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

11．設集合M={x|x²＞4}，N={x|x＜3}，則以下各式正確的是（　　）

A．

M∪N={x|x＜3}

B．

M∩N={x|2＜|x|＜3}

C．

M∩N={x|2＜x＜3}

D．

M∪N=R

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

8．已知數列{a_n}是等比數列，S_n為數列{a_n}的前n項和，且a₃=3，S₃=9
（1）求數列{a_n}的通項公式．
（2）設b_n=log₂$\frac{3}{{a}_{2n+3}}$，且{b_n}為遞增數列．若c_n=$\frac{8}{{b}_{n}{b}_{n+1}}$，求證：c₁+c₂+…+c_n＜2．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

9．設向量$\overrightarrow{a}$，$\overrightarrow{b}$不平行，向量λ$\overrightarrow{a}$+$\overrightarrow{b}$與$\overrightarrow{a}$+2$\overrightarrow{b}$平行，則實數λ=$\frac{1}{2}$．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學