
 如圖,等腰三角形ABC中,∠B=∠C,D在BC上,∠BAD大小為α,∠CAD大小為β.
如圖,等腰三角形ABC中,∠B=∠C,D在BC上,∠BAD大小為α,∠CAD大小為β.分析 (1)分別在△ABD和△ACD中使用正弦定理即可得出$\frac{BD}{DC}=\frac{sinα}{sinβ}$;
(2)利用三角恒等變換求出α,從而得出∠B.
解答 解:(1)在△ABD中,由正弦定理得$\frac{BD}{sinα}=\frac{AD}{sinB}$,
在△ACD中,由正弦定理得$\frac{DC}{sinβ}=\frac{AD}{sinC}$,
∵∠B=∠C,
∴$\frac{BD}{sinα}=\frac{DC}{sinβ}$,
∴$\frac{BD}{DC}=\frac{sinα}{sinβ}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{{\sqrt{6}}}{3}$.
(2)由(1)知$\frac{BD}{DC}$=$\frac{sinα}{sinβ}$=$\frac{1}{2}$,
又β=α+$\frac{π}{3}$,∴sinβ=sin($α+\frac{π}{3}$)=$\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα,
∴$\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα=2sinα,即$\sqrt{3}$cosα=3sinα,
∴tanα=$\frac{\sqrt{3}}{3}$,∴α=$\frac{π}{6}$,β=$\frac{π}{2}$,
∴B=$\frac{1}{2}$(π-α-β)=$\frac{π}{6}$.
點評 本題考查了正弦定理,三角恒等變換,屬于中檔題.


 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
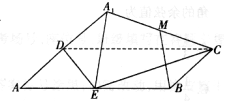 如圖,矩形ABCD中,AB=2BC=4,E為邊AB的中點,將△ADE沿直線DE翻轉成△A1DE.若M為線段A1C的中點,則在△ADE翻折過程中:
如圖,矩形ABCD中,AB=2BC=4,E為邊AB的中點,將△ADE沿直線DE翻轉成△A1DE.若M為線段A1C的中點,則在△ADE翻折過程中:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
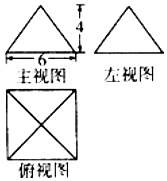 已知某幾何體的三視圖如圖所示,俯視圖是正方形,正視圖和側視圖都是底面邊長為6,高為4的等腰三角形.
已知某幾何體的三視圖如圖所示,俯視圖是正方形,正視圖和側視圖都是底面邊長為6,高為4的等腰三角形.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com