
 如圖,CD為△ABC外接圓的切線,AB的延長線交直線CD于點D,E,F分別為弦AB與弦AC上的點,且BC•AE=DC•AF,B,E,F,C四點共圓.證明:CA是△ABC外接圓的直徑.
如圖,CD為△ABC外接圓的切線,AB的延長線交直線CD于點D,E,F分別為弦AB與弦AC上的點,且BC•AE=DC•AF,B,E,F,C四點共圓.證明:CA是△ABC外接圓的直徑. 分析 B,E,F,C四點共圓,可得∠DBC=∠EAF.根據CD為△ABC外接圓的切線,可得∠BCD=∠FAE.由已知可證明:△BCD∽△FAE,可得∠DBC=∠EFA.可得∠CBA=90°.即可證明CA是△ABC外接圓的直徑.
解答 證明:∵B,E,F,C四點共圓,∴∠DBC=∠EAF.
∵CD為△ABC外接圓的切線,∴∠BCD=∠FAE.
在△BCD與△FAE中,
∵BC•AE=DC•AF,即$\frac{BC}{FA}$=$\frac{DC}{EA}$,又∠BCD=∠FAE.
∴△BCD∽△FAE,
∴∠DBC=∠EFA.
∴∠DBC=∠CBA,
又∠DBC+∠CBA=180°,
∴∠CBA=90°.
∴CA是△ABC外接圓的直徑.
點評 本題考查了四點共圓的性質、相似三角形的判定與性質定理、弦切角定理、圓的性質,考查了推理能力與計算能力,屬于中檔題.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD中,ABCD為平行四邊形,∠ABC=60°,AD=3,PA=AB=2,∠PAD=120°,點Q在線段AD上,DQ=1,點M在線段PB上,BP=3BM.
如圖,四棱錐P-ABCD中,ABCD為平行四邊形,∠ABC=60°,AD=3,PA=AB=2,∠PAD=120°,點Q在線段AD上,DQ=1,點M在線段PB上,BP=3BM.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 《九章算術》是我國古代的數學名著,體現了古代勞動人民的數學智慧,其中第六章“均輸”中,有一竹節容量問題,某人根據這一思想,設計了如圖所示的程序框圖,若輸出m的值為35,則輸入的a的值為5.
《九章算術》是我國古代的數學名著,體現了古代勞動人民的數學智慧,其中第六章“均輸”中,有一竹節容量問題,某人根據這一思想,設計了如圖所示的程序框圖,若輸出m的值為35,則輸入的a的值為5.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
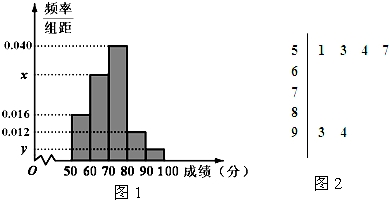
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(\frac{1}{4},+∞)$ | B. | (0,1) | C. | $(0,\frac{1}{2})$ | D. | $(0,\frac{1}{4})$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com