
 如圖,四棱錐P-ABCD中,ABCD為平行四邊形,∠ABC=60°,AD=3,PA=AB=2,∠PAD=120°,點(diǎn)Q在線段AD上,DQ=1,點(diǎn)M在線段PB上,BP=3BM.
如圖,四棱錐P-ABCD中,ABCD為平行四邊形,∠ABC=60°,AD=3,PA=AB=2,∠PAD=120°,點(diǎn)Q在線段AD上,DQ=1,點(diǎn)M在線段PB上,BP=3BM.分析 (Ⅰ)在BC上取點(diǎn)N,使CN=2,連接AN,AM,結(jié)合已知可得AQCN是平行四邊形,得AN∥CQ,則AN∥平面PCQ,再由平行線截線段成比例定理可得MN∥PC,得MN∥平面PCQ,由面面平行的判定可得平面AMN∥平面PCQ,得到AM∥平面PCQ;
(Ⅱ)取PQ中點(diǎn)E,連接AE,可得AE⊥PQ.求解三角形可得CQ⊥AD,由面面垂直的性質(zhì)得到CQ⊥平面PAD,進(jìn)一步得到AE⊥平面PCQ,得∠ACE為直線AC與平面PCQ所成角.求解直角三角形得答案.
解答 (Ⅰ)證明:在BC上取點(diǎn)N,使CN=2,連接AN,AM,
∵DQ=1,AD=3,AQ=2=CN,
∴AQCN是平行四邊形,則AN∥CQ,
∴AN∥平面PCQ,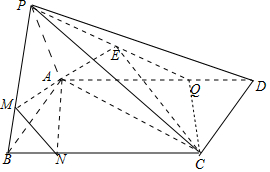
∵$\frac{BN}{BC}=\frac{BM}{BP}$=$\frac{1}{3}$,
∴MN∥PC,則MN∥平面PCQ,有平面AMN∥平面PCQ.
又∵AM?平面AMN,
∴AM∥平面PCQ;
(Ⅱ)解:取PQ中點(diǎn)E,連接AE,
∵PA=AQ,∴AE⊥PQ.
∵QD=1,CD=2,∠CDQ=60°,
∴CQ⊥AD,
∵平面PAD⊥平面ABCD,
∴CQ⊥平面PAD,
∴CQ⊥AE,又AE⊥PQ,
∴AE⊥平面PCQ,
∴∠ACE即為直線AC與平面PCQ所成角.
在Rt△AEC中,
∵AE=1,AC=$\sqrt{A{Q}^{2}+C{Q}^{2}}=\sqrt{7}$.
∴sin∠ACE=$\frac{AE}{AC}=\frac{\sqrt{7}}{7}$.
點(diǎn)評 本題考查線面平行的判定,考查直線與平面所成角,考查空間想象能力和思維能力,是中檔題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | M⊆N | B. | N⊆M | C. | M∪N=R | D. | M∩N=∅ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | k≠1且k≠-3 | B. | k≠-3 | C. | k=1 | D. | k=1且k=-3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 向左平移$\frac{π}{10}$個單位長度 | B. | 向右平移$\frac{π}{10}$個單位長度 | ||
| C. | 向左平移$\frac{π}{2}$個單位長度 | D. | 向右平移$\frac{π}{2}$個單位長度 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
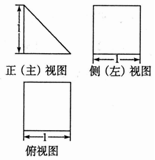 某幾何體的三視圖如圖所示,則該幾何體的體積為( )
某幾何體的三視圖如圖所示,則該幾何體的體積為( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 如圖,CD為△ABC外接圓的切線,AB的延長線交直線CD于點(diǎn)D,E,F(xiàn)分別為弦AB與弦AC上的點(diǎn),且BC•AE=DC•AF,B,E,F(xiàn),C四點(diǎn)共圓.證明:CA是△ABC外接圓的直徑.
如圖,CD為△ABC外接圓的切線,AB的延長線交直線CD于點(diǎn)D,E,F(xiàn)分別為弦AB與弦AC上的點(diǎn),且BC•AE=DC•AF,B,E,F(xiàn),C四點(diǎn)共圓.證明:CA是△ABC外接圓的直徑.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com