
分析 (Ⅰ)求出函數的導數,根據導數的幾何意義即可求出切線方程,
(Ⅱ)求出函數的導數,解關于導函數的方程,求出函數的單調區間即可,根據函數的單調性判斷即可;
(Ⅲ)原不等式轉化為blnx>m+$\frac{x}{2}$在區間[1,e]上恒成立,顯然該函數在[1,e]上單調遞增,從而最小值為0,從而要滿足條件,只需m+$\frac{x}{2}$<0,從而得到-$\frac{x}{2}$>m,同樣的辦法求在[1,e]上的最小值,只要該最小值大于m,從而可求出m的取值范圍
解答 解:(Ⅰ)當m=1時,g(x)=$\frac{1}{x}$+$\frac{1}{2}$,
∴g′(x)=-$\frac{1}{{x}^{2}}$,
∴k=g′(1)=-1,g(1)=1+$\frac{1}{2}$=$\frac{3}{2}$,
∴曲線y=g(x)在x=1處的切線方程為y-$\frac{3}{2}$=-(x-1),即2x+2y-5=0,
(Ⅱ)∵f(x)=$\frac{lnx}{x}$的定義域為(0,+∞),
∴f′(x)=$\frac{1-lnx}{{x}^{2}}$,令f′(x)=0,解得x=e,
當0<x<e時,f′(x)>0,函數f(x)單調遞增,
當x>e時,f′(x)<0,函數f(x)單調遞減,
∵2017>2016,
∴$\frac{ln2017}{2017}$<$\frac{ln2016}{2016}$,
即ln2017${\;}^{\frac{1}{2017}}$<ln2016${\;}^{\frac{1}{2016}}$,
∴2017${\;}^{\frac{1}{2017}}$<2016${\;}^{\frac{1}{2016}}$,
(Ⅲ)對于任意正實數b,關于x的不等式bf(x)>g(x)在區間[1,e]上恒成立,
∴bxf(x)>xg(x),
即blnx>m+$\frac{x}{2}$在區間[1,e]上恒成立,
當b>0,∴函數blnx在[1,e]上單調遞增;
∴x=1時,函數blnx取最小值0;
∴m+$\frac{x}{2}$<0,
∴-$\frac{x}{2}$>m在x∈[1,e]上恒成立;-$\frac{x}{2}$在[1,e]上的最小值為-$\frac{e}{2}$;
∴-$\frac{e}{2}$>m,即m<-$\frac{e}{2}$
∴實數m的取值范圍為(-∞,-$\frac{e}{2}$).
點評 本題考查根據導數的幾何意義,函數導數判斷函數單調性、求函數單調區間的方法,根據單調性求函數的最小值,屬于中檔題


 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | [-$\frac{47}{16}$,2] | B. | [-$\frac{47}{16}$,$\frac{39}{16}$] | C. | [-2$\sqrt{3}$,2] | D. | [-2$\sqrt{3}$,$\frac{39}{16}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,$\sqrt{2}$] | B. | (1,2] | C. | [$\sqrt{2}$,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 6 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x>1} | B. | {x|x<1} | C. | {x|0<x<1} | D. | {x|x>1或x<-1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
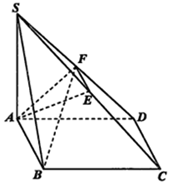 如圖,四邊形ABCD為矩形,SA⊥平面ABCD,E、F分別是SC、SD的中點,SA=AD=2,$AB=\sqrt{6}$
如圖,四邊形ABCD為矩形,SA⊥平面ABCD,E、F分別是SC、SD的中點,SA=AD=2,$AB=\sqrt{6}$查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com