
分析 (1)根據(jù)導(dǎo)數(shù)的幾何意義即可求出a的值,
(2)(i)先求導(dǎo),根據(jù)導(dǎo)數(shù)和函數(shù)的單調(diào)性即可判斷,
(ii)由H(x)=0,可得H(x1)=2lnx1-x12-ax1=0,H(x2)=2lnx2-x22-ax2=0,通過兩式相減,整理化簡可得a=$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-(x2+x1),再代入計(jì)算可得H′($\frac{{x}_{1}+{x}_{2}}{2}$)=-$\frac{2}{{x}_{2}-{x}_{1}}$[2ln$\frac{{x}_{2}}{{x}_{1}}$-$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$],然后換元,構(gòu)造函數(shù),根據(jù)導(dǎo)數(shù)和函數(shù)的最值即可證明
解答 解:(1)函數(shù)f(x)=2lnx-ax的導(dǎo)數(shù)為f′(x)=$\frac{2}{x}$-a,
可得f(x)在(2,f(2))處的切線斜率為k1=1-a;
g(x)=x2的導(dǎo)數(shù)為g′(x)=2x,
可得函數(shù)g(x)在(2,g(2))處的切線斜率為k2=4.
由切線平行,可得1-a=4,
解得a=-3.
(2)(i)H(x)=f(x)-g(x)=2lnx-ax-x2,
∴H′(x)=$\frac{2}{x}$-a-2x=-$\frac{2{x}^{2}+ax-2}{x}$,
易知當(dāng)x>1時(shí),H′(x)在[1,+∞)上單調(diào)遞減,
∴H′(x)≤H′(1)=-a,
當(dāng)a≥0時(shí),H′(x)≤0在[1,+∞)恒成立,
∴當(dāng)aa≥0時(shí),函數(shù)y=H(x)在[1,+∞]上的單調(diào)遞減,
(ii)∵x1,x2(x1<x2)是H(x)的兩個(gè)零點(diǎn),
∴H(x1)=2lnx1-x12-ax1=0,H(x2)=2lnx2-x22-ax2=0,
兩式相減可得2ln$\frac{{x}_{2}}{{x}_{1}}$-(x22-x12)-a(x2-x1)=0,
∴a=$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-(x2+x1),
∵H′(x)=$\frac{2}{x}$-a-2x,
∴H′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{4}{{x}_{1}+{x}_{2}}$-(x2+x1)-[$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-(x2+x1)]=-$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$+$\frac{4}{{x}_{1}+{x}_{2}}$=-$\frac{2}{{x}_{2}-{x}_{1}}$[2ln$\frac{{x}_{2}}{{x}_{1}}$-$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$]=-$\frac{2}{{x}_{2}-{x}_{1}}$[2ln$\frac{{x}_{2}}{{x}_{1}}$-$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$],
不妨設(shè)設(shè)t=ln$\frac{{x}_{2}}{{x}_{1}}$>1,構(gòu)造函數(shù)h(t)=lnt-$\frac{2(t-1)}{1+t}$,
則h′(t)=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴h(t)在(1,+∞)上是增函數(shù),
∴h(e)>h(1)=0,
∵-$\frac{2}{{x}_{2}-{x}_{1}}$<0,
∴H′($\frac{{x}_{1}+{x}_{2}}{2}$)<0
點(diǎn)評 本題考查了導(dǎo)數(shù)的幾何意義以及導(dǎo)數(shù)和函數(shù)的最值,以及函數(shù)零點(diǎn)的問題,以及不等式的證明,考查了學(xué)生的運(yùn)算能力和轉(zhuǎn)化能力,屬于難題



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
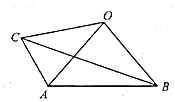 如圖,在四邊形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,則λ+μ的值為( )
如圖,在四邊形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,則λ+μ的值為( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com