
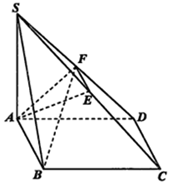
 如圖,四邊形ABCD為矩形,SA⊥平面ABCD,E、F分別是SC、SD的中點,SA=AD=2,$AB=\sqrt{6}$
如圖,四邊形ABCD為矩形,SA⊥平面ABCD,E、F分別是SC、SD的中點,SA=AD=2,$AB=\sqrt{6}$分析 (Ⅰ)推導出EF是△SCD的邊CD的中位線,從而EF∥CD,由四邊形ABCD為矩形,得CD∥AB,從而EF∥AB,由此能證明EF∥平面SAB.
(Ⅱ)推導出SD⊥AF,AB⊥SA,從而AB⊥平面SAD,進而SD⊥AB,由EF∥AB,得SD⊥EF,由此能證明SD⊥平面AEF.
(Ⅲ)EF⊥平面SAD,從而△AEF為直角三角形,求出${S_{△AEF}}=\frac{{\sqrt{3}}}{2}$,三棱錐S-AFE的高為SF=$\sqrt{2}$,由此能求出三棱錐S-AFE的體積.
解答 證明:(Ⅰ)∵E、F分別為SC、SD的中點,∴EF是△SCD的邊CD的中位線,
∴EF∥CD…(1分)
∵四邊形ABCD為矩形,∴CD∥AB,∴EF∥AB…(2分)
∵AB?平面SAB,EF?平面SAB,
∴EF∥平面SAB.…(4分)
(Ⅱ)∵SA=AD,F為SD的中點,∴SD⊥AF,…(5分)
∵SA⊥平面ABCD,AB?平面ABCD,∴AB⊥SA,
∵AB⊥AD,SA,AD是平面SAD內的兩條相交直線,
∴AB⊥平面SAD,
∵SD?平面SAD,∴SD⊥AB,…(7分)
∵EF∥AB,∴SD⊥EF,…(8分)
∵AF、EF是平面AEF內的兩條相交直線,
∴SD⊥平面AEF.…(9分)
解:(Ⅲ)由(Ⅱ)知EF⊥平面SAD,
∴△AEF為直角三角形,∴${S_{△AEF}}=\frac{{\sqrt{3}}}{2}$,…(11分)
∵三棱錐S-AFE的高為SF=$\sqrt{2}$,
∴三棱錐S-AFE的體積$\frac{{\sqrt{6}}}{6}$.…(13分)
點評 本題考查線面平行、線面垂直的證明,考查幾何體的體積的求法,考查推理論證能力、運算求解能力、空間想象能力,考查數形結合思想、化歸與轉化思想、函數與方程思想,考查創新意識、應用意識,是中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
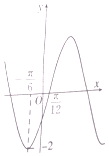
| A. | $(kπ-\frac{π}{6},kπ+\frac{π}{3}),k∈Z$ | B. | $(2kπ-\frac{π}{6},2kπ+\frac{π}{3}),k∈Z$ | ||
| C. | $(2kπ+\frac{π}{3},2kπ+\frac{5π}{6}),k∈Z$ | D. | $(kπ+\frac{π}{3},kπ+\frac{5π}{6}),k∈Z$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
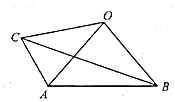 如圖,在四邊形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,則λ+μ的值為( )
如圖,在四邊形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,則λ+μ的值為( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | $[\frac{1}{8},+∞)$ | C. | $[-1,\frac{1}{8}]$ | D. | $[\frac{1}{8},1]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
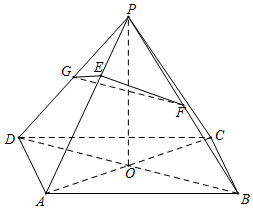 四棱錐P-ABCD中,底面ABCD是邊長為2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,點F,G分別是線段PB,PD上的中點,E在PA上,且PA=3PE.
四棱錐P-ABCD中,底面ABCD是邊長為2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,點F,G分別是線段PB,PD上的中點,E在PA上,且PA=3PE.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com