综合中文字幕,久久97视频,久久成人精品

精英家教網 > 高中數學 > 題目詳情

4．在1907年的一項關于16艘輪船的研究中，船的噸位區間從192t～3246t，船員的人數從5人到32人，由船員人數關于噸位的回歸分析得到如下結果：$\widehat{y}$=9.5+0.0062x，假定的兩艘輪船的噸位相差1000t，船員平均人數相差6人，對于最小的船估計的船員人數是11人，對于最大的船估計的船員人數是31人．

分析根據回歸方程，計算兩艘輪船噸位相差1000噸時船員平均人數的差值，
以及x=192和x=3246t時，對應$\widehat{y}$的值即可．

解答解：由題意，由于船員人數關于噸位的回歸方程是：
$\widehat{y}$=9.5+0.0062x，
兩艘輪船噸位相差1000噸時，
船員平均人數的差值是0.0062×1000≈6（人）；
當x=192t時，由回歸方程計算$\widehat{y}$=9.5+0.0062×192≈11（人）；
當x=3246t時，由回歸方程計算$\widehat{y}$=9.5+0.0062×3246≈31（人）；
所以，兩艘輪船的噸位相差1000t，船員平均人數相差6人，
對于最小的船估計的船員人數是11人，對于最大的船估計的船員人數是31人．
故答案為：6，11，31．

點評本題考查了線性回歸方程的應用問題，是基礎題．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：解答題

6．設函數f（x）=e^x+sinx（e為自然對數的底數），g（x）=ax，F（x）=f（x）-g（x）．
（1）若a=2，且直線x=t（t≥0）分別與函數f（x）和g（x）的圖象交于P，Q，求P，Q兩點間的最短距離；
（2）若x≥0時，函數y=F（x）的圖象恒在y=F（-x）的圖象上方，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

7．已知α∈[0，π），在直角坐標系xOy中，直線l₁的參數方程為$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t為參數）；在以坐標原點O為極點，x軸的正半軸為極軸的極坐標系中，直線l₂的極坐標方程是ρcos（θ-α）=2sin（α+$\frac{π}{6}$）．
（Ⅰ）求證：l₁⊥l₂
（Ⅱ）設點A的極坐標為（2，$\frac{π}{3}$），P為直線l₁，l₂的交點，求|OP|•|AP|的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

4．

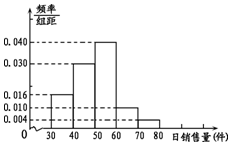某超市計劃銷售某種產品，先試銷該產品n天，對這n天日銷售量進行統計，得到頻率分布直方圖如圖．
（Ⅰ）若已知銷售量低于50的天數為23，求n；
（Ⅱ）廠家對該超市銷售這種產品的日返利方案為：每天固定返利45元，另外每銷售一件產品，返利3元；頻率估計為概率．依此方案，估計日返利額的平均值．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

11．已知點P在橢圓C₁：$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{4}$=1上，點Q在橢圓C₂：$\frac{{y}^{2}}{9}$+x²=1上，O為坐標原點，記ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$，集合{（P，Q）|ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$}，當ω取得最大值時，集合中符合條件的元素有幾個（　　）

A．

2個

B．

4個

C．

8個

D．

無數個

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

9．求棱長為a的正四面體的內切球和外接球的體積之比．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

16．已知命題p：?x＜1，$log{\;}_{\frac{1}{3}}x＜0$；命題q：?x₀∈R，$x_0^2≥{2^{x_0}}$，則下列命題中為真命題的是（　　）

A．

p∨q

B．

（￢p）∧（￢q）

C．

p∨（￢q）

D．

p∧q

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

13．某種產品的廣告費用支出x（萬元）與銷售額y（萬元）之間有如下的對應數據：

x	2	4	6	8	10
y	40	50	70	90	100

（1）請根據上表提供的數據，用最小二乘法求出y關于x 的線性回歸方程$\stackrel{∧}{y}$=bx+a

p（K²≥k）	…	0.10	0.05	0.025	0.010	0.005	0.001	…
k	…	2.706	3.841	5.024	6.635	7.879	10.828	…

（其中：b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$　）求回歸直線方程．
（2）據此估計廣告費用為12時，銷售收入y的值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

14．已知函數f（x）=lnx-mx²+（1-2m）x+1
（I）當m=1時，求曲線f（x）在點（1，f（1））處的切線方程；
（II）若m∈Z，關于x的不等式f（x）≤0恒成立，求m的最小值．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學