
| A. | 最大值為1 | B. | 圖象關于直線x=-$\frac{π}{2}$對稱 | ||
| C. | 既是奇函數又是周期函數 | D. | 圖象關于點($\frac{3π}{4}$,0)中心對稱 |
分析 根據題意逐一判斷各個選項是否正確,從而得出結論.
解答 解:∵函數f(x)=sinxcos2x,當x=$\frac{3π}{2}$時,f(x)取得最大值為1,故A正確;
當x=-$\frac{π}{2}$時,函數f(x)=1,為函數的最大值,故圖象關于直線x=-$\frac{π}{2}$對稱;故B正確;
函數f(x)滿足f(-x)=sin(-x)cos(-2x)=-sinxcos2x=-f(x),故函數f(x)為奇函數,
再根據f(x+2π)=sin(x+2π)cos[-2(x+2π)]=sinxcos2x,故f(x)的周期為2π,故C正確;
由于f($\frac{3π}{2}$-x)+f(x)=-cosx•cos(3π-2x)+sinxcos2x=cosxcos2x+sinxcos2x=cos2x(sinx+cosx)=0不一定成立,
故f(x)圖象不一定關于點($\frac{3π}{4}$,0)中心對稱,故D不正確,
故選:D.
點評 本題考查三角函數的對稱性,考查了三角函數值域的解法,考查排除法在選擇題中的應用,屬于中檔題.


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:解答題
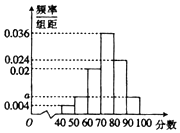 某高校在舉行藝術類高考招生考試時,對100個考生進行了一項專業水平考試,考試成績滿分為100分,成績出來后,老師對每個成績段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人數進行了統計,丙得到如圖所示的頻率分布直方圖.
某高校在舉行藝術類高考招生考試時,對100個考生進行了一項專業水平考試,考試成績滿分為100分,成績出來后,老師對每個成績段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人數進行了統計,丙得到如圖所示的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com