
分析 (I)由a2>a1>0?${a}_{1}+\frac{2}{a}$-1>a1>0,解得0<a1<2.又a3>a2>0,?${a}_{2}+\frac{2}{{a}_{2}-1}$>a2,?0<a2<2?$0<{a}_{1}+\frac{2}{{a}_{1}}$-1<2,解得1<a1<2.可得:1<a1<2.下面利用數學歸納法證明:當1<a1<2時,?n∈N*,1<an<2成立即可.于是an+1-an=$\frac{2}{{a}_{n}}$-1>0,即an+1>an,滿足{an}是遞增數列,即可得出a1的取值范圍.
(II)a1>2,可用數學歸納法證明:an>2對?n∈N*都成立.于是:an+1-an=$\frac{2}{{a}_{n}}$-1<2,即數列{an}是遞減數列.在Sn≥na1-$\frac{1}{3}$(n-1)中,令n=2,可得:2a1+$\frac{2}{{a}_{1}}$-1=S2≥2a1-$\frac{1}{3}$,解得a1≤3,因此2<a1≤3.
下證:(1)當$2<{a}_{1}≤\frac{7}{3}$時,Sn≥na1-$\frac{1}{3}$(n-1)恒成立.事實上,當$2<{a}_{1}≤\frac{7}{3}$時,由an=a1+(an-a1)≥a1+(2-$\frac{7}{3}$)=${a}_{1}-\frac{1}{3}$.累加求和即可證明.
再證明:(2)${a}_{1}>\frac{7}{3}$時不合題意.事實上,當$\frac{7}{3}<{a}_{1}≤3$時,設an=bn+2,可得$\frac{1}{3}<{b}_{1}$≤1.由an+1=an+$\frac{2}{{a}_{n}}$-1(n∈N*),可得:bn+1=bn+$\frac{2}{{b}_{n}}$-1,可得$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{b}_{n}+1}{{b}_{n}+2}$≤$\frac{{b}_{1}+1}{{b}_{1}+2}$≤$\frac{2}{3}$.于是數列{bn}的前n和Tn≤3.故Sn=2n+Tn<2n+3=na1+(2-a1)n+3,令a1=$\frac{7}{3}$+t(t>0),可得:Sn<na1-$\frac{1}{3}(n-1)$.這與Sn≥na1-$\frac{1}{3}$(n-1)恒成立矛盾.
解答 (I)解:由a2>a1>0?${a}_{1}+\frac{2}{a}$-1>a1>0,解得0<a1<2,①.
又a3>a2>0,?${a}_{2}+\frac{2}{{a}_{2}-1}$>a2,?0<a2<2?$0<{a}_{1}+\frac{2}{{a}_{1}}$-1<2,解得1<a1<2,②.
由①②可得:1<a1<2.
下面利用數學歸納法證明:當1<a1<2時,?n∈N*,1<an<2成立.
(1)當n=1時,1<a1<2成立.
(2)假設當n=k∈N*時,1<an<2成立.
則當n=k+1時,ak+1=ak+$\frac{2}{{a}_{k}}$-1∈$[2\sqrt{2}-1,2)$?(1,2),
即n=k+1時,不等式成立.
綜上(1)(2)可得:?n∈N*,1<an<2成立.
于是an+1-an=$\frac{2}{{a}_{n}}$-1>0,即an+1>an,
∴{an}是遞增數列,a1的取值范圍是(1,2).
(II)證明:∵a1>2,可用數學歸納法證明:an>2對?n∈N*都成立.
于是:an+1-an=$\frac{2}{{a}_{n}}$-1<2,即數列{an}是遞減數列.
在Sn≥na1-$\frac{1}{3}$(n-1)中,令n=2,可得:2a1+$\frac{2}{{a}_{1}}$-1=S2≥2a1-$\frac{1}{3}$,解得a1≤3,因此2<a1≤3.
下證:(1)當$2<{a}_{1}≤\frac{7}{3}$時,Sn≥na1-$\frac{1}{3}$(n-1)恒成立.
事實上,當$2<{a}_{1}≤\frac{7}{3}$時,由an=a1+(an-a1)≥a1+(2-$\frac{7}{3}$)=${a}_{1}-\frac{1}{3}$.
于是Sn=a1+a2+…+an≥a1+(n-1)$({a}_{1}-\frac{1}{3})$=na1-$\frac{1}{3}(n-1)$.
再證明:(2)${a}_{1}>\frac{7}{3}$時不合題意.
事實上,當$\frac{7}{3}<{a}_{1}≤3$時,設an=bn+2,可得$\frac{1}{3}<{b}_{1}$≤1.
由an+1=an+$\frac{2}{{a}_{n}}$-1(n∈N*),可得:bn+1=bn+$\frac{2}{{b}_{n}}$-1,可得$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{b}_{n}+1}{{b}_{n}+2}$≤$\frac{{b}_{1}+1}{{b}_{1}+2}$≤$\frac{2}{3}$.
于是數列{bn}的前n和Tn≤${b}_{1}•\frac{1-(\frac{2}{3})^{n}}{1-\frac{2}{3}}$<3b1≤3.
故Sn=2n+Tn<2n+3=na1+(2-a1)n+3,③.
令a1=$\frac{7}{3}$+t(t>0),由③可得:Sn<na1+(2-a1)n+3=na1-$\frac{1}{3}(n-1)$-tn+$\frac{8}{3}$.
只要n充分大,可得:Sn<na1-$\frac{1}{3}(n-1)$.這與Sn≥na1-$\frac{1}{3}$(n-1)恒成立矛盾.
∴${a}_{1}>\frac{7}{3}$時不合題意.
綜上(1)(2)可得:$2<{a}_{1}≤\frac{7}{3}$,于是可得$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{b}_{n}+1}{{b}_{n}+2}$≤$\frac{{b}_{1}+1}{{b}_{1}+2}$≤$\frac{4}{7}$.(由$2<{a}_{1}≤\frac{7}{3}$可得:$0<{b}_{1}≤\frac{1}{3}$).
故數列{bn}的前n項和Tn≤${b}_{1}•\frac{1-(\frac{4}{7})^{n}}{1-\frac{4}{7}}$<$\frac{7}{3}$b1<1,∴Sn=2n+Tn<2n+1.
點評 本題考查了等差數列與等比數列的通項公式及其求和公式、數列遞推關系、分類討論方法、數列的單調性、數學歸納法,考查了推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:選擇題
| A. | 最大值為1 | B. | 圖象關于直線x=-$\frac{π}{2}$對稱 | ||
| C. | 既是奇函數又是周期函數 | D. | 圖象關于點($\frac{3π}{4}$,0)中心對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
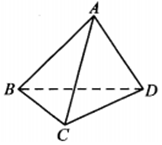 在四面體ABCD中,二面角A-BC-D為60°,點P為直線BC上一動點,記直線PA與平面BCD所成的角為θ,則( )
在四面體ABCD中,二面角A-BC-D為60°,點P為直線BC上一動點,記直線PA與平面BCD所成的角為θ,則( )| A. | θ的最大值為60° | B. | θ的最小值為60° | C. | θ的最大值為30° | D. | θ的最小值為30° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=ln(-x)+2x+1 | B. | f(x)=-ln(-x)-2x+1 | C. | f(x)=-ln(-x)-2x-1 | D. | f(x)=-ln(-x)+2x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{23}{4}$ | B. | $\frac{23}{4}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com