Question

20．某濕地公園有一邊長為4百米的正方形水域ABCD，如圖，EF是其中軸線，水域正中央有一半徑為1百米的圓形島嶼M，小島上種植有各種花卉．現欲在線段AF上某點P處（AP的長度不超過1百米）開始建造一直線觀光木橋與小島邊緣相切（不計木橋寬度），與BC相交于Q點．過Q點繼續建造直線木橋NQ與小島邊緣相切，NQ與中軸線EF交于N點，N點與E點也以木橋直線相連．
（1）當AP=1百米時，求木橋PQ的長度（單位：百米）；
（2）問是否存在常數m，使得mQN+NE為定值？如果存在，請求出常數m，并給出定值，如果不存在，請說明理由．

Answer 1

分析 （1）設PQ斜率為k，根據直線PQ與圓M相切列方程解出k，得出Q點坐標，從而可計算PQ的長；
（2）設PQ斜率為k，NQ斜率為k₁，AP=a，根據切線的性質得出k，k₁與a的關系，求出mNQ+NE，化簡即可得出結論．

解答 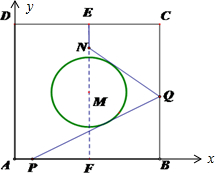解：（1）以A為原點，AB所在直線為x軸，
建立平面直角坐標系如圖（單位：百米）．
圓M的方程為：（x-2）²+（y-2）²=1，P（1，0），
設直線PQ的方程為y=k（x-1），則$\frac{|k-2|}{\sqrt{{k}^{2}+1}}$=1，
解得k=$\frac{3}{4}$，∴直線PQ的方程為y=$\frac{3}{4}$（x-1），
把x=4代入直線方程得y=$\frac{9}{4}$，即Q（4，$\frac{9}{4}$），
∴PQ=$\sqrt{P{B}^{2}+B{Q}^{2}}$=$\frac{15}{4}$．
答：木橋PQ的長度為$\frac{15}{4}$百米．
（2）設AP=a百米，（0≤a≤1），
設PQ方程為y=k（x-a），則$\frac{|k（2-a）-2|}{\sqrt{{k}^{2}+1}}$=1，
∴2-k（2-a）=$\sqrt{{k}^{2}+1}$，
設直線NQ斜率為k₁，則直線NQ的方程為y-k（4-a）=k₁（x-4），
令x=2得N（2，k（4-a）-2k₁），
∴NE=4+2k₁-k（4-a），
∵直線NQ與圓M相切，∴$\frac{|{k}_{1}（2-4）-2+k（4-a）|}{\sqrt{1+{{k}_{1}}^{2}}}$=1，
∴-2k₁-2+k（4-a）=$\sqrt{{{k}_{1}}^{2}+1}$，
∴NQ=$\sqrt{1+{{k}_{1}}^{2}}$|4-2|=2$\sqrt{1+{{k}_{1}}^{2}}$=2[-2k₁-2+k（4-a）]，
∴mNQ+NE=2m[-2k₁-2+k（4-a）]+4+2k₁-k（4-a）=（1-2m）[2+2k₁-k（4-a）]+2，
∴當1-2m=0，即m=$\frac{1}{2}$時，$\frac{1}{2}$NQ+NE=2．
答：存在常數m=$\frac{1}{2}$，使得$\frac{1}{2}$NQ+NE為定值2．

點評 本題考查了直線與圓的位置關系，距離公式的應用，屬于中檔題．