
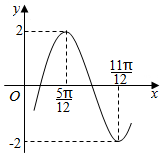
 函數f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分圖象如圖所示,則f(x)的單調遞增區間為( )
函數f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分圖象如圖所示,則f(x)的單調遞增區間為( )| A. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z) |
分析 由函數圖象可求函數的周期T,利用周期公式可求ω,由題意2sin(2×$\frac{5π}{12}$+φ)=2,解得φ=2kπ-$\frac{π}{3}$,k∈Z,結合范圍-$\frac{π}{2}$<φ<$\frac{π}{2}$,可求φ,解得函數解析式,利用正弦函數的單調性即可得解.
解答 解:由函數圖象可得:$\frac{1}{2}$T=$\frac{11π}{12}$-$\frac{5π}{12}$=π,
∴ω=2,
∵函數f(x)的圖象過點($\frac{5π}{12}$,2),
∴2sin(2×$\frac{5π}{12}$+φ)=2,
∴$\frac{5π}{6}$+φ=2kπ+$\frac{π}{2}$,k∈Z,可得:φ=2kπ-$\frac{π}{3}$,k∈Z,
∵-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴當,φ=0時,φ=-$\frac{π}{3}$,可得:f(x)=2sin(2x-$\frac{π}{3}$),
∴令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,可得:kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,k∈Z,
故選:B.
點評 本題主要考查了由y=Asin(ωx+φ)的部分圖象確定其解析式,考查了正弦函數的單調性,屬于基礎題.


科目:高中數學 來源: 題型:解答題
| 甲 | 80 | 110 | 135 | 135 | 140 |
| 乙 | 100 | x | y | 125 | 155 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 相切 | B. | 相交 | C. | 相離 | D. | 不確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|0<x≤3} | B. | {x|3≤x<4} | C. | {x|0<x<4} | D. | {x|-4≤x<4} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,+∞) | B. | (-∞,2) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{6}{13}$ | B. | $\frac{6}{13}$ | C. | $-\frac{17}{13}$ | D. | $\frac{17}{13}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{7}$ | C. | $\sqrt{7}$或1 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com