
分析 由題意易得an=2n+1(n∈N),進而可得bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n+1)(2n+3}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),由裂項相消法可得結果
解答 解:∵數列{an}的前n項和為Sn,且Sn=n2+2n,
∴n=1時,a1=3;
n≥2時,an=Sn-Sn-1=2n+1,
∴an=2n+1(n∈N*),
∴bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
Tn=b1+b2+…bn=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2n+1}$-$\frac{1}{2n+3}$)=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{2n+3}$)=$\frac{n}{3(2n+3)}$,
故答案為:$\frac{n}{3(2n+3)}$.
點評 本題考查等差數列的前n項和與通項公式的關系,涉及裂項相消法求數列的和,屬中檔題.


 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
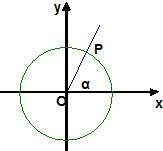 已知角α的終邊與單位圓的交點是P(x0,y0)
已知角α的終邊與單位圓的交點是P(x0,y0)查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (4,9) | B. | (-4,-9) | C. | (4,-9) | D. | (-4,9) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{15}{11}$ | C. | -1 | D. | $\frac{17}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
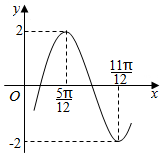 函數f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分圖象如圖所示,則f(x)的單調遞增區間為( )
函數f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分圖象如圖所示,則f(x)的單調遞增區間為( )| A. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
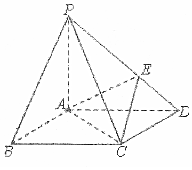 在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,點E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.
在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,點E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com