Question

19．如圖，四棱錐P-ABCD中，PC=AD=CD=$\frac{1}{2}$AB=1，AB∥DC，AD⊥CD，PC⊥平面ABCD．
（Ⅰ）求證：BC⊥平面PAC；
（Ⅱ）若M為線段PA的中點，且過C，D，M三點的平面與線段PB交于點N，確定點N的位置，并說明理由．

Answer 1

分析 （I）連接AC，推導出AC⊥BC，PC⊥BC，由此能證明BC⊥平面PAC．
（II）當N為PB的中點時，由M為PA的中點，得到MN∥AB，且MN=$\frac{1}{2}AB=2a$．再由AB∥CD，得MN∥CD從而求出點N為過C，D，M三點的平面與線段PB的交點．

解答 解：（I）連接AC，在直角梯形ABCD中，AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{2}$，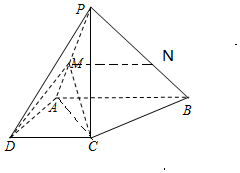
BC=$\sqrt{（AB-CD）^{2}+A{D}^{2}}$=$\sqrt{2}$，
∴AC²+BC²=AB²，即AC⊥BC．
又PC⊥平面ABCD，∴PC⊥BC，
又AC∩PC=C，故BC⊥平面PAC．
解：（II）N為PB的中點．
理由如下：
∵N為PB的中點，M為PA的中點，
∴MN∥AB，且MN=$\frac{1}{2}AB=2a$．
又∵AB∥CD，∴MN∥CD，∴M，N，C，D四點共面，
∴點N為過C，D，M三點的平面與線段PB的交點．

點評 本題考查線面垂直的證明，考查點的位置的確定，考查空間中線線、線面、面面間的位置關系等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、數形結合思想，是中檔題．