
分析 (1)由復數m2-1+(m+1)i是實數,可得m+1=0,解得m.
(2)由復數$z=(\sqrt{x}-1)+({x^2}-3x+2)i$的對應點位于第二象限,可得$\left\{\begin{array}{l}{\sqrt{x}-1<0}\\{{x}^{2}-3x+2>0}\end{array}\right.$,x≥0,解出即可得出.
解答 解:(1)∵復數m2-1+(m+1)i是實數,∴m+1=0,解得m=-1.
(2)∵復數$z=(\sqrt{x}-1)+({x^2}-3x+2)i$的對應點位于第二象限,
∴$\left\{\begin{array}{l}{\sqrt{x}-1<0}\\{{x}^{2}-3x+2>0}\end{array}\right.$,x≥0,解得0<x<1.
∴實數x的取值范圍為[0,1).
點評 本題考查了復數為實數的充要條件、復數的幾何意義、不等式的解法,考查了推理能力與計算能力,屬于基礎題.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:解答題
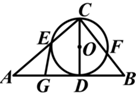 如圖,已知CD是△ABC中AB邊上的高,以CD為直徑的⊙O分別交CA、CB于點E、F,點G是AD的中點.$GE=BD=2,EC=\frac{9}{5}$.
如圖,已知CD是△ABC中AB邊上的高,以CD為直徑的⊙O分別交CA、CB于點E、F,點G是AD的中點.$GE=BD=2,EC=\frac{9}{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com