日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
14．f（x）是偶函數，且在（-∞，0）上是增函數，則下列關系成立的是（　　）
A．f（-2）＜f（1）＜f（3）B．f（1）＜f（-2）＜f（3）C．f（3）＜f（-2）＜f（1）D．f（-2）＜f（3）＜f（1）

分析 由已知中函數f（x）在（-∞，0）上為增函數，結合函數f（x）是偶函數，可得答案．

解答 解：∵f（x）是偶函數，且在（-∞，0）上是增函數，
∴f（3）=f（-3）＜f（-2）＜f（1）=f（-1），
故選：C．

點評 本題考查的知識點是抽象函數及其應用，函數的單調性，函數的奇偶性，難度中檔．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：選擇題

4．已知曲線C1：y2=tx（y＞0，t＞0）在點M（$\frac{4}{t}$，2）處的切線與曲線C2：y=ex+1-1也相切，則tln$\frac{4{e}^{2}}{t}$的值為（　　）
A．4e2B．8eC．2D．8

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

5．設U=R，M={y|y=2x+1，-$\frac{1}{2}$≤x≤$\frac{1}{2}$}，N={x|y=lg（x2+3x）}，則（∁UM）∩N=（　　）
A．（-∞，-3]∪（2，+∞）B．（-∞，-3）∪（0，+∞）C．（-∞，-3）∪（2，+∞）D．（-∞，0）∪（2，+∞）

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

2．下列命題中正確的是（　　）
A．若p∨q為真命題，則p∧q為真命題．
B．“x=5”是“x2-4x-5=0”的必要不充分條件．
C．命題“?x∈R，x2+x-1＜0”的否定為：“?x∈R，x2+x-1≥0”．
D．命題“已知A，B為一個三角形兩內角，若A=B，則sinA=sinB”的否命題為真命題．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

9．給出下列結論：
（1）函數f（x）=tanx有無數個零點；
（2）集合A={x|y=2x+1}，集合 B={x|y=x2+x+1}則A∩B={（0，1），（1，3）}；
（3）函數$f（x）=\frac{1}{2}sinx+\frac{1}{2}|{sinx}|$的值域是[-1，1]；
（4）函數$f（x）=2sin（2x+\frac{π}{3}）$的圖象的一個對稱中心為$（\frac{π}{3}，0）$；
（5）已知函數f（x）=2cosx，若存在實數x1，x2，使得對任意的實數x都有f（x1）≤f（x）≤f（x2）成立，則|x1-x2|的最小值為2π．
其中結論正確的序號是（1）（4）（把你認為結論正確的序號都填上）．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

19．函數y=x2-sinx在x=0處的切線方程為y=-x．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

6．設$\overrightarrow{a}$，$\overrightarrow{b}$，是任意的非零平面向量，且相互不共線，則下列正確的是（　　）
A．若向量$\overrightarrow{a}$，$\overrightarrow{b}$滿足|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|，且$\overrightarrow{a}$，$\overrightarrow{b}$同向，則$\overrightarrow{a}$＞$\overrightarrow{b}$
B．|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|
C．|$\overrightarrow{a}$•$\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$|
D．|$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$|

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

3．已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1，F2為橢圓的左．右焦點，M是橢圓上任一點，若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$的取值范圍為[-3，3]，則橢圓方程為（　　）
A．$\frac{x^2}{9}+\frac{y^2}{3}=1$B．$\frac{x^2}{6}+\frac{y^2}{3}=1$C．$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1D．$\frac{{x}^{2}}{4}$+y2=1

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

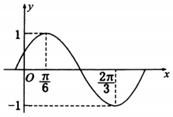4．函數f（x）=Asin（ωx+φ）（A＞0，ω，0，|φ|＜$\frac{π}{2}$）的部分圖象如圖所示．
（Ⅰ）求函數f（x）的解析式；
（Ⅱ）若函數F（x）=3[f（x-$\frac{π}{12}$）]2+mf（x-$\frac{π}{12}$）+2在區間[0，$\frac{π}{2}$]上有四個不同零點，求實數m的取值范圍．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 一级片免费网站 | 国产精品成人一区二区三区 | 国产亚洲欧美一区二区 | 成人爽a毛片一区二区免费 www.欧美精品 | 国产美女一区二区三区 | 亚洲黄色三级 | 中文字幕+乱码+中文乱码91 | 中文字幕无人区二 | 国产精品久久免费 | 国产亚洲欧美在线 | 日韩免费一级片 | 国产人人干 | 色婷婷香蕉在线一区二区 | 欧美在线视频一区二区 | 国产一级片视频 | 黄色一级大片 | 亚洲乱码在线 | 一级片免费 | 欧美日韩免费一区二区三区 | 欧美日韩一区二区在线观看 | 99re国产精品 | 国产精品自拍小视频 | 黄色三级在线 | 黄色网址在线播放 | 亚洲一区日韩 | 91禁蘑菇在线看 | 91av免费在线观看 | 久久精品一区二区 | 亚洲黄色精品 | 天天天操| 国产美女视频 | 性色av一区| 成人免费视屏 | 久久综合一区 | 久久99精品久久久久久琪琪 | 日韩一区在线视频 | 二区三区在线观看 | 黄色大片网站 | 不卡的av网站 | www久久| 欧美一区二区三 |