Question

8．已知直線l：x-y=1與圓M：x²+y²-2x+2y=0相交于A，C兩點，點B，D分別在圓M上運動，且位于直線AC兩側，則四邊形ABCD面積的最大值為2$\sqrt{3}$．

Answer 1

分析 先求出弦長|AB|的長度，然后結合圓與直線的位置關系圖象，然后將ABCD的面積看成兩個三角形△ABC和△ACD的面積之和，分析可得當BD為AC的垂直平分線時，四邊形ABCD的面積最大．

解答 解：把圓Γ：x²+y²-2x+2y-1=0化為標準方程：（x-1）²+（y+1）²=2，圓心（1，-1），半徑r=$\sqrt{2}$．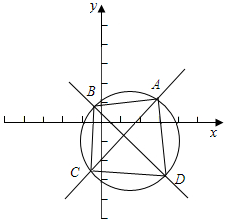
直線與圓相交，由點到直線的距離公式的弦心距d=$\frac{\sqrt{2}}{2}$．
由勾股定理的弦長|AB|=2$\sqrt{{r}^{2}-p9vv5xb5^{2}}$=$\frac{\sqrt{6}}{2}$×$2=\sqrt{6}$，
又B，D兩點在圓上，并且位于直線l的兩側，
四邊形ABCD的面積可以看成是兩個三角形△ABC和△ACD的面積之和，
如圖所示，當B，D為如圖所示位置，即BD為弦AC的垂直平分線時（即為直徑時），
兩三角形的面積之和最大，即四邊形ABCD的面積最大，
最大面積為：S=$\frac{1}{2}$×|AB|×|CE|+$\frac{1}{2}$×|AB|×|DE|=$\frac{1}{2}$|AB|•|CD|=$\frac{1}{2}×\sqrt{6}×2\sqrt{2}$=2$\sqrt{3}$，
故答案為：2$\sqrt{3}$．

點評 本題涉及到圓與位置關系的題目，可采用數形結合思想，實現代數和幾何間的轉化，然后分析題目具體問題，求解即可，屬于中檔題