
分析 由雙曲線的標準方程可知:則x=2secα,y=tanα,由3x2-2xy=12sec2α-4secαtanα=$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$,由-1<sinα<1,1-sinα>0,1+sinα>0,由基本不等式的性質可知∴[(1-sinα)+(1+sinα)]•($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$)≥12+2$\sqrt{\frac{4(1+sinα)}{1-sinα}×\frac{8(1-sinα)}{1+sinα}}$=12+8$\sqrt{2}$,則$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$≥6+4$\sqrt{2}$,即可求得3x2-2xy的最小值.
解答 解:由線$\frac{{x}^{2}}{4}$-y2=1,設x=2secα,y=tanα,
3x2-2xy=12sec2α-4secαtanα,
=$\frac{12}{co{s}^{2}α}$-$\frac{4sinα}{co{s}^{2}α}$,
=$\frac{12-4sinα}{co{s}^{2}α}$
=$\frac{12-4sinα}{1-si{n}^{2}α}$,
=$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$
∵-1<sinα<1,
1-sinα>0,1+sinα>0
∴[(1-sinα)+(1+sinα)]•($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$),
=12+$\frac{4(1+sinα)}{1-sinα}$+$\frac{8(1-sinα)}{1+sinα}$≥12+2$\sqrt{\frac{4(1+sinα)}{1-sinα}×\frac{8(1-sinα)}{1+sinα}}$=12+8$\sqrt{2}$,
當且僅當$\frac{4(1+sinα)}{1-sinα}$=$\frac{8(1-sinα)}{1+sinα}$等號成立,
解得:sinα=3-2$\sqrt{2}$(3+2$\sqrt{2}$舍去)時,取得最小值,
∵[(1-sinα)+(1+sinα)]•($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$)=2($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$),
$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$≥6+4$\sqrt{2}$,
∴3x2-2xy的最小值是6+4$\sqrt{2}$,
故答案為:6+4$\sqrt{2}$.
點評 本題考查雙曲線的參數方程,三角恒等變換,基本不等式性質的綜合應用,考查計算能力,屬于難題.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
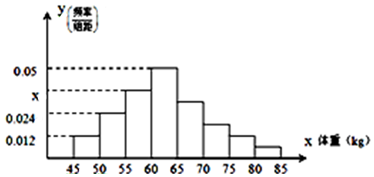
| A. | 0.044 | B. | 0.039 | C. | 0.01 | D. | 0.04 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A=B | B. | A∩B=∅ | C. | A∩B=A | D. | A∪B=A |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com