
| A. | 關于直線x=1對稱 | B. | 關于直線y=x對稱 | ||
| C. | 關于直線y=-1對稱 | D. | 關于直線y=1對稱 |
分析 將y=log${\;}_{\frac{1}{3}}$(9x)換成3為底,結合對數函數的圖象可得答案.
解答 解:由題意:y=log${\;}_{\frac{1}{3}}$(9x)換成3為底的對數,
可得:y=-log39x=y=-(log3x+log332)=log${\;}_{\frac{1}{3}}$x-2.
結合對數函數的圖象,可得:log${\;}_{\frac{1}{3}}$x-2與y=log3x關于直線y=-1對稱,
即函數y=log3x與y=log${\;}_{\frac{1}{3}}$(9x)的圖象關于直線y=-1對稱,
故選C.
點評 本題考查了對數函數的圖象的畫法和平移問題.屬于基礎題.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(sinA)<f(sinB) | B. | f(cosA)>f(cosB) | C. | f(sinA)<f(cosB) | D. | f(sinA)>f(cosB) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
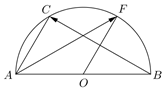 以AB為直徑的半圓,|$\overrightarrow{AB}$|=2,O為圓心,C是$\widehat{AB}$上靠近點A的三等分點,F是$\widehat{AB}$上的某一點,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,則$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.
以AB為直徑的半圓,|$\overrightarrow{AB}$|=2,O為圓心,C是$\widehat{AB}$上靠近點A的三等分點,F是$\widehat{AB}$上的某一點,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,則$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com