
| A. | f(sinA)<f(sinB) | B. | f(cosA)>f(cosB) | C. | f(sinA)<f(cosB) | D. | f(sinA)>f(cosB) |
分析 先求導(dǎo),求出函數(shù)的單調(diào)減區(qū)間,再根據(jù)誘導(dǎo)公式和三角形的內(nèi)角的關(guān)系得到答案.
解答 解:f′(x)=3x2-3,
令f′(x)=0,解得x=±1,
當(dāng)f′(x)≤0時(shí),即-1≤x≤1時(shí),函數(shù)單調(diào)遞減,
∵△ABC中,C為鈍角,
∴90°<C<180°,
∴0<B+A<90°,
∴0<B<90°-A<90°,
∴sinB<sin(90°-A)=cosA,cosB>cos(90°-A)=sinA,
∴f(sinB)>f(cosA),f(cosB)>f(sinA),
∵A,B的大小無(wú)法判斷,
∴sinA與sinB,cosA與cosB無(wú)法判斷,
故選:C
點(diǎn)評(píng) 本題考查了導(dǎo)數(shù)和函數(shù)的單調(diào)性的關(guān)系和三角形中的角的關(guān)系和三角函數(shù)的值域以及單調(diào)性,屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | △PF1F2的內(nèi)切圓的圓心必在直線x=a上 | |
| B. | △PF1F2的內(nèi)切圓的圓心必在直線x=b上 | |
| C. | △PF1F2的內(nèi)切圓的圓心必在直線OP上 | |
| D. | △PF1F2的內(nèi)切圓必通過(guò)點(diǎn)(b,0) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (1,5) | B. | (-3,1) | C. | (5,7] | D. | (-3,7] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
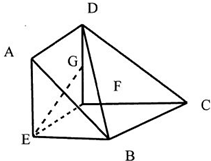 已知直角梯形ABCD中,AD⊥AB,AB∥DC,AB=2,DC=3,E為AB的中點(diǎn),過(guò)E作EF∥AD,將四邊形AEFD沿EF折起使面AEFD⊥面EBCF.
已知直角梯形ABCD中,AD⊥AB,AB∥DC,AB=2,DC=3,E為AB的中點(diǎn),過(guò)E作EF∥AD,將四邊形AEFD沿EF折起使面AEFD⊥面EBCF.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (-∞,2] | B. | [2,+∞) | C. | [2,$\frac{7}{2}$] | D. | [$\frac{7}{2}$,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 關(guān)于直線x=1對(duì)稱 | B. | 關(guān)于直線y=x對(duì)稱 | ||
| C. | 關(guān)于直線y=-1對(duì)稱 | D. | 關(guān)于直線y=1對(duì)稱 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com