Question

5．已知y=f（x）是定義在R上的奇函數，f（x）=$\left\{\begin{array}{l}{（x+2）^{2}-1，x＜-1}\\{0，-1≤x≤0}\end{array}\right.$，且當函數y=f（x-1）-$\frac{1}{2}$-k（x-2）（其中k＞0）的零點個數取得最大值時，則實數k的取值范圍是（$\frac{1}{4}，6-\sqrt{30}$）．（$\sqrt{2}≈$1.414，$\sqrt{30}$≈5.477）

Answer 1

分析 由已知函數的奇偶性及函數解析式作出函數y=f（x-1）的圖象，把函數y=f（x-1）-$\frac{1}{2}$-k（x-2）（其中k＞0）的零點個數轉化為y=k（x-2）+$\frac{1}{2}$與y=f（x-1）的圖象交點的個數，數形結合得答案．

解答 解：∵y=f（x）是定義在R上的奇函數，且f（x）=$\left\{\begin{array}{l}{（x+2）^{2}-1，x＜-1}\\{0，-1≤x≤0}\end{array}\right.$，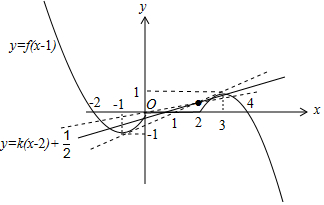
∴y=f（x-1）的圖象如圖所示：
y=k（x-2）+$\frac{1}{2}$表示過點（2，$\frac{1}{2}$），斜率為k的直線，
由圖可得，y=k（x-2）+$\frac{1}{2}$與y=f（x-1）的圖象最多有5個交點，
即函數y=f（x-1）-$\frac{1}{2}$-k（x-2）至多有5個零點．
當k=$\frac{1}{4}$時，直線y=k（x-2）+$\frac{1}{2}$過原點，此時y=k（x-2）+$\frac{1}{2}$與y=f（x-1）的圖象有4個交點，
即函數y=f（x-1）-$\frac{1}{2}$-k（x-2）有4個零點；
當k=6-$\sqrt{30}$時，直線y=k（x-2）+$\frac{1}{2}$與y=f（x-1）的圖象拋物線部分相切，此時y=k（x-2）+$\frac{1}{2}$
與y=f（x-1）的圖象有4個交點，即函數y=f（x-1）-$\frac{1}{2}$-k（x-2）有3個零點．
故當函數y=f（x-1）-$\frac{1}{2}$-k（x-2）（其中k＞0）的零點個數取得最大值時，k∈（$\frac{1}{4}，6-\sqrt{30}$）．
故答案為：（$\frac{1}{4}，6-\sqrt{30}$）．

點評 本題考查根的存在性與根的個數判斷，考查數學轉化思想方法與數形結合的解題思想方法，是中檔題．