
分析 直線的普通方程為x=$\frac{1}{2}$,圓的普通方程為x2+y2=1,求出圓心(0,0)到直線x=$\frac{1}{2}$的距離d=$\frac{1}{2}$,由此能求出直線$ρcosθ=\frac{1}{2}$被圓ρ=1所截得的弦長.
解答 解:直線$ρcosθ=\frac{1}{2}$的普通方程為x=$\frac{1}{2}$,
圓ρ=1的x2+y2=1,
圓心(0,0)到直線x=$\frac{1}{2}$的距離d=$\frac{1}{2}$,
∴直線$ρcosθ=\frac{1}{2}$被圓ρ=1所截得的弦長:
|AB|=2$\sqrt{1-(\frac{1}{2})^{2}}$=$\sqrt{3}$.
故答案為:$\sqrt{3}$.
點評 本題考查直線被圓截得的弦長的求法,考查直角坐標方程、極坐標方程、參數方程的互化等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想,是中檔題.


科目:高中數學 來源: 題型:選擇題
 如圖,網格紙上小正方形的邊長為1,粗線畫出的一個三棱錐的三視圖,則該三棱錐的表面積為( )
如圖,網格紙上小正方形的邊長為1,粗線畫出的一個三棱錐的三視圖,則該三棱錐的表面積為( )| A. | $\frac{{15+\sqrt{17}}}{2}$ | B. | $\frac{{13+\sqrt{17}}}{2}$ | C. | $\frac{{11+\sqrt{17}}}{2}$ | D. | $\frac{{9+\sqrt{17}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
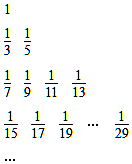 把數列{$\frac{1}{2n-1}$}的所有數按照從大到小的原則寫成如圖,第k行有2k-1個數,第t行的第s個數(從左數起)記為A(t,s),則A(6,10)=( )
把數列{$\frac{1}{2n-1}$}的所有數按照從大到小的原則寫成如圖,第k行有2k-1個數,第t行的第s個數(從左數起)記為A(t,s),則A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 2$\sqrt{13}$ | C. | 2$\sqrt{5}$ | D. | 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com