Question

8．定義域為R的偶函數f（x）滿足?x∈R，有f（x+2）=f（x）-f（1），且當x∈[2，3]時，f（x）=-2x²+12x-18，若函數y=f（x）-log_a（x+1）恰有三個零點，則a的取值范圍是（　　）

• A． （0，$\frac{\sqrt{5}}{5}$）
• B． （0，$\frac{\sqrt{3}}{3}$）
• C． （$\frac{\sqrt{5}}{5}$，$\frac{\sqrt{3}}{3}$）
• D． （$\frac{\sqrt{6}}{6}$，$\frac{\sqrt{5}}{5}$）

Answer 1

分析 由題意可得函數f（x）的周期為2，當x∈[2，3]時，f（x）=-2x²+12x-18，令g（x）=log_a（x+1），則f（x）的圖象和g（x）的圖象恰有3個交點，畫出圖形，數形結合，根據g（2）＞f（2），且f（4）＞g（4），求得a的取值范圍．

解答 解：∵f（x+2）=f（x）-f（1），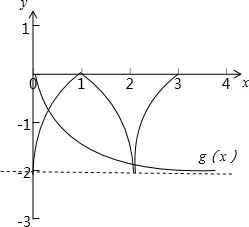
且f（x）是定義域為R的偶函數，
令x=-1可得f（-1+2）=f（-1）-f（1），
又f（-1）=f（1），
可得f（1）=0 則有，f（x+2）=f（x），
∴f（x）是周期為2的偶函數．
當x∈[2，3]時，f（x）=-2x²+12x-18=-2（x-3）²，
函數f（x）的圖象為開口向下、頂點為（3，0）的拋物線．
函數y=f（x）-log_a（x+1）在（0，+∞）上恰有三個零點，
令g（x）=log_a（x+1），則f（x）的圖象和g（x）的圖象恰有3個交點．
作出函數的圖象，如圖所示，
∵f（x）≤0，∴g（x）≤0，可得0＜a＜1．
要使函數y=f（x）-log_a（|x|+1）在（0，+∞）上恰有三個零點，
則有g（2）＞f（2）且f（4）＞g（4），即 log_a（2+1）＞f（2）=-2，且-2＞log_a（4+1），
解得$\frac{\sqrt{5}}{5}$＜a＜$\frac{\sqrt{3}}{3}$．
故選：C．

點評 此題主要考查函數周期性及其應用，解題的過程中用到了數形結合的方法，這也是高考常考的熱點問題，屬于中檔題．