
分析 由已知可得,|PF1|+|PF2|=4,|PF1|•|PF2|=2.然后結合勾股定理及橢圓定義列式求得m值.
解答 解:由題意,|PF1|+|PF2|=4,且$\frac{1}{2}$|PF1|•|PF2|=1,即|PF1|•|PF2|=2.
且$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}$=$|{F}_{1}{F}_{2}{|}^{2}$=4(4-m),
則$(|P{F}_{1}|+|P{F}_{2}|)^{2}=16$,
即$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}+2|P{F}_{1}|•|P{F}_{2}|=16$,
∴16-4m+2×2=16,解得m=1.
故答案為:1.
點評 本題考查橢圓的簡單性質,考查了橢圓定義的應用,是基礎的計算題.


科目:高中數學 來源: 題型:解答題
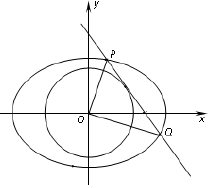 如圖,已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{2}}}{2}$,點(2,1)在橢圓C上.
如圖,已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{2}}}{2}$,點(2,1)在橢圓C上.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3x-5y+13=0 | B. | 5x+3y-1=0 | C. | 5x+3y+1=0 | D. | 5x-3y+11=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
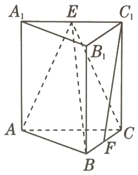 如圖,在三棱柱ABC-A1B1C1中,側棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分別為A1C1,BC的中點.
如圖,在三棱柱ABC-A1B1C1中,側棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分別為A1C1,BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com