
分析 由余弦定理求出BC=2$\sqrt{7}$,由正弦定理,求出sinB=$\frac{\sqrt{3}}{\sqrt{7}}$,從而cosB=$\frac{2}{\sqrt{7}}$,設AD=BD=x,由余弦定理得:cosB=$\frac{1}{x}$,由此能求出AD的值.
解答 解: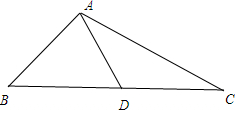 ∵在△ABC中,∠BAC=120°,AC=2AB=4,
∵在△ABC中,∠BAC=120°,AC=2AB=4,
∴由余弦定理得BC=$\sqrt{16+4-2×2×4×120°}$=2$\sqrt{7}$,
由正弦定理,得:$\frac{BC}{sinA}=\frac{AC}{sinB}$,
∴sinB=$\frac{AC•sinA}{BC}$=$\frac{4•sin120°}{2\sqrt{7}}$=$\frac{\sqrt{3}}{\sqrt{7}}$,
∴cosB=$\sqrt{1-(\frac{\sqrt{3}}{\sqrt{7}})^{2}}$=$\frac{2}{\sqrt{7}}$,
∵AD=BD,∴設AD=BD=x,
由余弦定理得:cosB=$\frac{4+{x}^{2}-{x}^{2}}{2×2×x}$=$\frac{1}{x}$,
∴AD=x=$\frac{1}{cosB}$=$\frac{\sqrt{7}}{2}$.
故答案為:$\frac{{\sqrt{7}}}{2}$.
點評 本題考查三角形邊長的求法,涉及到正弦定理、余弦定理等基礎知識,考查推理論證能力、運算求解能力,考查函數與方思想、數形結合思想,是中檔題.


 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | π-2 | B. | 2π-4 | C. | 3π-6 | D. | 4π-8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
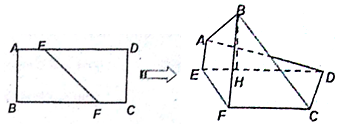
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
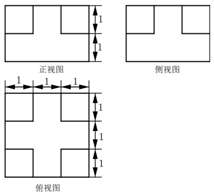 榫卯(sǔn mǎo)是古代中國建筑、家具及其它器械的主要結構方式,是在兩個構件上采用凹凸部位相結合的一種連接方式,凸出部分叫做“榫頭”.某“榫頭”的三視圖及其部分尺寸如圖所示,則該“榫頭”體積等于( )
榫卯(sǔn mǎo)是古代中國建筑、家具及其它器械的主要結構方式,是在兩個構件上采用凹凸部位相結合的一種連接方式,凸出部分叫做“榫頭”.某“榫頭”的三視圖及其部分尺寸如圖所示,則該“榫頭”體積等于( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com