
分析 (1)化切為弦,兩邊同乘ρ,結合公式x=ρcosθ,y=ρsinθ可得曲線C的直角坐標方程;直角把直線l的參數方程消去參數t可得其普通方程;
(2)聯立直線方程與拋物線方程,求得M、N的橫坐標,把|PM|=|MN|轉化為橫坐標的關系求m值.
解答 解:(1)由ρ•sinθ•tanθ=4m,得ρsin2θ=4mcosθ,即ρ2sin2θ=4mρcosθ,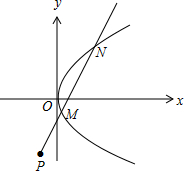
∴y2=4mx(m>0),
故曲線C的直角坐標方程為y2=4mx(m>0),
由$\left\{{\begin{array}{l}{x=-1+tcos{{45}°}}\\{y=-2+tsin{{45}°}}\end{array}}\right.$,得$\left\{\begin{array}{l}{x=-1+\frac{\sqrt{2}}{2}t}\\{y=-2+\frac{\sqrt{2}}{2}t}\end{array}\right.$,①
消去參數t得:x-y-1=0,
故直線l的普通方程為x-y-1=0;
(2)如圖,聯立$\left\{\begin{array}{l}{y=x+1}\\{{y}^{2}=4mx}\end{array}\right.$,得x2+(2-4m)x+1=0.
解得:${x}_{1}=2m-1-2\sqrt{{m}^{2}-m}$,${x}_{2}=2m-1+2\sqrt{{m}^{2}-m}$.
由題意可得:$2m-1-2\sqrt{{m}^{2}-m}+1$=$4\sqrt{{m}^{2}-m}$,解得m=$\frac{9}{8}$(m>0).
點評 本題考查參數方程化普通方程,考查了簡單曲線的極坐標方程,體現了數形結合的解題思想方法,是中檔題.


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
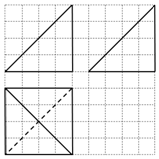 某空間幾何體的三視圖如圖所示(圖中小正方形的邊長為1),則這個幾何體的體積是( )
某空間幾何體的三視圖如圖所示(圖中小正方形的邊長為1),則這個幾何體的體積是( )| A. | 16 | B. | 32 | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若m∥α,n⊥β且α⊥β,則m∥n | B. | 若m⊥α,n⊥β且α⊥β,則m⊥n | ||
| C. | 若α⊥β,α∩β=m,n⊥m,則n⊥β | D. | 若α∩β=m,n?α,m⊥n,則α⊥β |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com