
分析 (1)曲線C轉化為ρ2sin2θ=2aρcosθ,(a>0),由此能求出曲線C的普通方程;l的參數方程消去參數能求出l的直角坐標方程.
(2)將l的參數方程代入曲線C的普通方程,得:${t}^{2}-2\sqrt{2}at+8a=0$,由根的差別式得a>4,由韋達定理得${t}_{1}+{t}_{2}=2\sqrt{2}a$,t1t2=8a,由此利用|PM|,|MN|,|PN|成等比數列,能求出a.
解答 解:(1)∵曲線C:ρsin2θ=2acosθ(a>0),∴ρ2sin2θ=2aρcosθ,(a>0),
∴曲線C的普通方程為y2=2ax,(a>0);
∵l的參數方程為:$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(t為參數),
∴消去參數得l的直角坐標方程為:x-y+2=0.
(2)將l的參數方程:$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(t為參數)代入y2=2ax,(a>0),
得:${t}^{2}-2\sqrt{2}at+8a=0$,
△=8a2-32a>0,解得a>4,
${t}_{1}+{t}_{2}=2\sqrt{2}a$,t1t2=8a,
∵|PM|,|MN|,|PN|成等比數列,
∴|t1-t2|2=|t1t2|,∴(2$\sqrt{2}a$)2-4×8a=8a,
解得a=5.
點評 本題考查曲線的普通方程與直線的直角坐標方程的求法,考查實數值的求法,涉及到直角坐標方程、極坐標方程、參數方程的互化、根的判別式、韋達定理、等比數列等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


科目:高中數學 來源: 題型:解答題
| 積極參加班級工作 | 不太主動參加班級工作 | 合計 | |
| 學習積極性高 | |||
| 學習積極性一般 | |||
| 合計 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
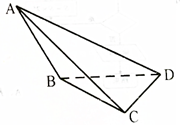 如圖所示,在三棱錐A-BCD中,側面ABD,ACD是全等的直角三角形,AD是公共的斜邊且AD=$\sqrt{3}$,BD=CD=1,另一側面ABC是正三角形.
如圖所示,在三棱錐A-BCD中,側面ABD,ACD是全等的直角三角形,AD是公共的斜邊且AD=$\sqrt{3}$,BD=CD=1,另一側面ABC是正三角形.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | ±$\sqrt{2}$ | C. | ±2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{6}$,2] | D. | [$\frac{1}{9}$,2] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com