
| A. | E(ξ1)<E(ξ2),D(ξ1)<D(ξ2) | B. | E(ξ1)<E(ξ2),D(ξ1)>D(ξ2) | C. | E(ξ1)>E(ξ2),D(ξ1)<D(ξ2) | D. | E(ξ1)>E(ξ2),D(ξ1)>D(ξ2) |
分析 由已知得0<p1<p2<$\frac{1}{2}$,$\frac{1}{2}$<1-p2<1-p1<1,求出E(ξ1)=p1,E(ξ2)=p2,從而求出D(ξ1),D(ξ2),由此能求出結(jié)果.
解答 解:∵隨機(jī)變量ξi滿足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2,…,
0<p1<p2<$\frac{1}{2}$,
∴$\frac{1}{2}$<1-p2<1-p1<1,
E(ξ1)=1×p1+0×(1-p1)=p1,
E(ξ2)=1×p2+0×(1-p2)=p2,
D(ξ1)=(1-p1)2p1+(0-p1)2(1-p1)=${p}_{1}-{{p}_{1}}^{2}$,
D(ξ2)=(1-p2)2p2+(0-p2)2(1-p2)=${p}_{2}-{{p}_{2}}^{2}$,
D(ξ1)-D(ξ2)=p1-p12-(${p}_{2}-{{p}_{2}}^{2}$)=(p2-p1)(p1+p2-1)<0,
∴E(ξ1)<E(ξ2),D(ξ1)<D(ξ2).
故選:A.
點(diǎn)評(píng) 本題考查離散型隨機(jī)變量的數(shù)學(xué)期望和方差等基礎(chǔ)知識(shí),考查推理論證能力、運(yùn)算求解能力、空間想象能力,考查數(shù)形結(jié)合思想、化歸與轉(zhuǎn)化思想,是中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 若p∧q為假命題,則p∨q為真命題 | |
| B. | 不存在實(shí)數(shù)α,β,使得等式tanα+tanβ=tan(α+β)成立 | |
| C. | 函數(shù)f(x)=ax2+bx+c為偶函數(shù)的充要條件是 b=0 | |
| D. | 若定義在R上的函數(shù)f(x)滿足f(x)•f(x+1)=1,則f(x)是一個(gè)周期為1的函數(shù) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
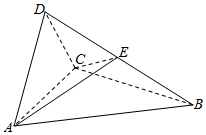 如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD. 查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com