
分析 (1)求導,根據導數與函數單調性的關系,分類討論,即可求得f(x)單調性;
(2)由(1)可知:當a>0時才有兩個零點,根據函數的單調性求得f(x)最小值,由f(x)min<0,g(a)=alna+a-1,a>0,求導,由g(a)min=g(e-2)=e-2lne-2+e-2-1=-$\frac{1}{{e}^{2}}$-1,g(1)=0,即可求得a的取值范圍.
(1)求導,根據導數與函數單調性的關系,分類討論,即可求得f(x)單調性;
(2)分類討論,根據函數的單調性及函數零點的判斷,分別求得函數的零點,即可求得a的取值范圍.
解答 解:(1)由f(x)=ae2x+(a-2)ex-x,求導f′(x)=2ae2x+(a-2)ex-1,
當a=0時,f′(x)=-2ex-1<0,
∴當x∈R,f(x)單調遞減,
當a>0時,f′(x)=(2ex+1)(aex-1)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$),
令f′(x)=0,解得:x=ln$\frac{1}{a}$,
當f′(x)>0,解得:x>ln$\frac{1}{a}$,
當f′(x)<0,解得:x<ln$\frac{1}{a}$,
∴x∈(-∞,ln$\frac{1}{a}$)時,f(x)單調遞減,x∈(ln$\frac{1}{a}$,+∞)單調遞增;
當a<0時,f′(x)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$)<0,恒成立,
∴當x∈R,f(x)單調遞減,
綜上可知:當a≤0時,f(x)在R單調減函數,
當a>0時,f(x)在(-∞,ln$\frac{1}{a}$)是減函數,在(ln$\frac{1}{a}$,+∞)是增函數;
(2)①若a≤0時,由(1)可知:f(x)最多有一個零點,
當a>0時,f(x)=ae2x+(a-2)ex-x,
當x→-∞時,e2x→0,ex→0,
∴當x→-∞時,f(x)→+∞,
當x→∞,e2x→+∞,且遠遠大于ex和x,
∴當x→∞,f(x)→+∞,
∴函數有兩個零點,f(x)的最小值小于0即可,
由f(x)在(-∞,ln$\frac{1}{a}$)是減函數,在(ln$\frac{1}{a}$,+∞)是增函數,
∴f(x)min=f(ln$\frac{1}{a}$)=a×($\frac{1}{{a}^{2}}$)+(a-2)×$\frac{1}{a}$-ln$\frac{1}{a}$<0,
∴1-$\frac{1}{a}$-ln$\frac{1}{a}$<0,即ln$\frac{1}{a}$+$\frac{1}{a}$-1>0,
設t=$\frac{1}{a}$,則g(t)=lnt+t-1,(t>0),
求導g′(t)=$\frac{1}{t}$+1,由g(1)=0,
∴t=$\frac{1}{a}$>1,解得:0<a<1,
∴a的取值范圍(0,1).
方法二:(1)由f(x)=ae2x+(a-2)ex-x,求導f′(x)=2ae2x+(a-2)ex-1,
當a=0時,f′(x)=2ex-1<0,
∴當x∈R,f(x)單調遞減,
當a>0時,f′(x)=(2ex+1)(aex-1)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$),
令f′(x)=0,解得:x=-lna,
當f′(x)>0,解得:x>-lna,
當f′(x)<0,解得:x<-lna,
∴x∈(-∞,-lna)時,f(x)單調遞減,x∈(-lna,+∞)單調遞增;
當a<0時,f′(x)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$)<0,恒成立,
∴當x∈R,f(x)單調遞減,
綜上可知:當a≤0時,f(x)在R單調減函數,
當a>0時,f(x)在(-∞,-lna)是減函數,在(-lna,+∞)是增函數;
(2)①若a≤0時,由(1)可知:f(x)最多有一個零點,
②當a>0時,由(1)可知:當x=-lna時,f(x)取得最小值,f(x)min=f(-lna)=1-$\frac{1}{a}$-ln$\frac{1}{a}$,
當a=1,時,f(-lna)=0,故f(x)只有一個零點,
當a∈(1,+∞)時,由1-$\frac{1}{a}$-ln$\frac{1}{a}$>0,即f(-lna)>0,
故f(x)沒有零點,
當a∈(0,1)時,1-$\frac{1}{a}$-ln$\frac{1}{a}$<0,f(-lna)<0,
由f(-2)=ae-4+(a-2)e-2+2>-2e-2+2>0,
故f(x)在(-∞,-lna)有一個零點,
假設存在正整數n0,滿足n0>ln($\frac{3}{a}$-1),則f(n0)=${e}^{{n}_{0}}$(a${e}^{{n}_{0}}$+a-2)-n0>${e}^{{n}_{0}}$-n0>${2}^{{n}_{0}}$-n0>0,
由ln($\frac{3}{a}$-1)>-lna,
因此在(-lna,+∞)有一個零點.
∴a的取值范圍(0,1).
點評 本題考查導數的綜合應用,考查利用導數求函數單調性及最值,考查函數零點的判斷,考查計算能力,考查分類討論思想,屬于中檔題.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:選擇題
| A. | E(ξ1)<E(ξ2),D(ξ1)<D(ξ2) | B. | E(ξ1)<E(ξ2),D(ξ1)>D(ξ2) | C. | E(ξ1)>E(ξ2),D(ξ1)<D(ξ2) | D. | E(ξ1)>E(ξ2),D(ξ1)>D(ξ2) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
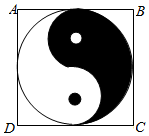 如圖,正方形ABCD內的圖形來自中國古代的太極圖.正方形內切圓中的黑色部分和白色部分關于正方形的中心成中心對稱.在正方形內隨機取一點,則此點取自黑色部分的概率是( )
如圖,正方形ABCD內的圖形來自中國古代的太極圖.正方形內切圓中的黑色部分和白色部分關于正方形的中心成中心對稱.在正方形內隨機取一點,則此點取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com