
 如圖所示,直三棱柱ABC-A1B1C1的各條棱長均為a,D是側棱CC1的中點.
如圖所示,直三棱柱ABC-A1B1C1的各條棱長均為a,D是側棱CC1的中點.分析 (1)取AB1的中點E,AB的中點F.連接DE、EF、CF.證明DE的平行線CF垂直平面ABB1A1,內的相交直線AB,BB1,即可證明平面AB1D⊥平面ABB1A1;
(2)建立空間直角坐標系,求平面AB1D的一個法向量,以及平面ABC的一個法向量,利用向量的數量積求平面AB1D與平面ABC所成二面角(銳角)的大小.
解答 證明:(1)取AB1的中點E,AB的中點F.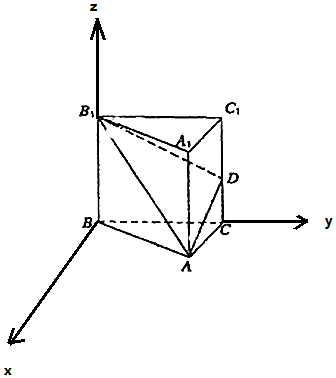
連接DE、EF、CF.
∵直三棱柱ABC-A1B1C1的各條棱長均為a,D是側棱CC1的中點,
∴EF$\underset{∥}{=}$$\frac{1}{2}$BB1,CD$\underset{∥}{=}$$\frac{1}{2}$BB1.
∴四邊形CDEF為平行四邊形,∴DE∥CF.
又三棱柱ABC-A1B1C1是直三棱柱.
△ABC為正三角形.CF?平面ABC,
∴CF⊥BB1,CF⊥AB,而AB∩BB1=B,∴CF⊥平面ABB1A1,
又DE∥CF,∴DE⊥平面ABB1A1.
又DE?平面AB1D.所以平面AB1D⊥平面ABB1A1.
解:(2)建立如圖所示的空間直角坐標系,
則A($\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$,0),C(0,a,0),D(0,a,$\frac{a}{2}$)B1(0,0,a),B(0,0,0),
$\overrightarrow{A{B}_{1}}$=(-$\frac{\sqrt{3}a}{2}$,-$\frac{a}{2}$,a),$\overrightarrow{AD}$=(-$\frac{\sqrt{3}a}{2},\frac{a}{2},\frac{a}{2}$),
設$\overrightarrow{n}$=(1,x,y)為平面AB1D的一個法向量.
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=-\frac{\sqrt{3}a}{2}-\frac{ax}{2}+ay=0}\\{\overrightarrow{n}•\overrightarrow{AD}=-\frac{\sqrt{3}a}{2}+\frac{ax}{2}+\frac{ay}{2}=0}\end{array}\right.$,解得$\overrightarrow{n}$=(1,$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),
平面ABC的一個法向量為$\overrightarrow{m}$=(0,0,1).
設平面AB1D與平面ABC所成二面角(銳角)為θ,
則cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\frac{2\sqrt{3}}{3}}{\sqrt{\frac{8}{3}}}$=$\frac{\sqrt{2}}{2}$,
∴θ=$\frac{π}{4}$.
∴平面AB1D與平面ABC所成二面角(銳角)的大小為$\frac{π}{4}$.
點評 本題考查平面與平面垂直的判定,二面角及其度量,考查空間想象能力,計算能力,是中檔題.證明平面與平面垂直主要轉化為證明一個平面內的一條直線與另一個平面垂直即可,而證明直線與平面垂直,只需證明此直線與平面圖內的兩條相交直線垂直;求二面角的大小新教材主要要求學生掌握用空間向量的方法來求:第一步建立適當的空間直角坐標系,并設出點的坐標;第二步分別求出二面角的兩個面的一個法向量;第三步代公式$cos\left?{\overrightarrow m,\overrightarrow n}\right>=\frac{|\overrightarrow m•\overrightarrow n|}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}$即可求得,注意運算的準確性.


科目:高中數學 來源: 題型:選擇題
| A. | 31 | B. | 15 | C. | 32 | D. | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 很小的實數可以構成集合 | |
| B. | 自然數集N中最小的數是1 | |
| C. | 集合{y|y=x2-1}與{(x,y)|y=x2-1}是同一個集合 | |
| D. | 空集是任何集合的子集 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
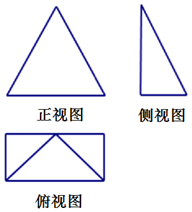 一個空間幾何體的三視圖如右圖,其中正視圖是邊長為2的正三角形,俯視圖是邊長分別為1,2的矩形,則該幾何體的側面積為4+$\sqrt{3}$.
一個空間幾何體的三視圖如右圖,其中正視圖是邊長為2的正三角形,俯視圖是邊長分別為1,2的矩形,則該幾何體的側面積為4+$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 32 | B. | 10+10$\sqrt{2}$ | C. | 20 | D. | 28 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 計算小于100的奇數的連乘積 | |
| B. | 計算從1開始的連續奇數的連乘積 | |
| C. | 從1開始的連續奇數的連乘積,當乘積大于100時,計算奇數的個數 | |
| D. | 計算1×3×5×…×n≥100時的最小的n值. |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com