
分析 (1)根據橢圓的定義可求出軌跡方程;
(2)設P(cosα,$\sqrt{2}$sinα),代入距離公式,利用二次函數的性質求出d(a);
(3)分別表示出S1及S2,由正數m滿足S1≤mS2得出m2≥$\frac{{{a}^{2}-a}^{4}}{8({a}^{2}+1)^{2}}$,利用換元法和二次函數的性質得出右側式子的最大值即可求出m的最小值.
解答 解:(1)設動圓的圓心坐標為C(x,y),則動圓的半徑r=|CF|
圓E的圓心為E(0,-1),半徑為2$\sqrt{2}$,
∵動圓與圓E內切,∴|CE|+|CF|=2$\sqrt{2}$,
∴動圓C的圓心軌跡為以E,F為焦點的橢圓,
設此橢圓方程為$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$,
則$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}={c}^{2}}\\{c=1}\\{2a=2\sqrt{2}}\end{array}\right.$,解得a=$\sqrt{2}$,b=1.
∴動圓的圓心的軌跡方程為$\frac{{y}^{2}}{2}+{x}^{2}$=1.
(2)設P(cosα,$\sqrt{2}$sinα),則|PA|2=(cosα-a)2+2sin2α
=-cos2α-2acosα+a2+2=-(cosα+a)2+2a2+2
①若-1≤a≤1,則當cosα=-a時,|PA|2取得最大值2a2+2,∴d(a)=$\sqrt{2{a}^{2}+2}$,
②若-a≤-1,即a≥1,則當cosα=-1時,|PA|2取得最大值-(a-1)2+2a2+2=a2+2a+1=(a+1)2,
∴d(a)=$\sqrt{(a+1)^{2}}$=|a+1|=a+1;
③若-a≥1,即a≤-1,則當cosα=1時,|PA|2取得最大值-(a+1)2+2a2+2=a2-2a+1=(a-1)2,
∴d(a)=$\sqrt{(a-1)^{2}}$=|a-1|=1-a.
綜上,d(a)=$\left\{\begin{array}{l}{\sqrt{2{a}^{2}+2},-1≤a≤1}\\{a+1,a>1}\\{1-a,a<1}\end{array}\right.$.
(3)把x=a代入$\frac{{y}^{2}}{2}+{x}^{2}$=1得y=±$\sqrt{2-{2a}^{2}}$,∴不妨設P(a,$\sqrt{2-2{a}^{2}}$),
則S1=S△POA=$\frac{1}{2}×a×\sqrt{2-2{a}^{2}}$,
由(2)可知d(a)=$\sqrt{2{a}^{2}+2}$,∴S2=d2(a)=2a2+2,
∵S1≤mS2,∴m≥$\frac{{S}_{1}}{{S}_{2}}$=$\frac{a\sqrt{2-2{a}^{2}}}{4({a}^{2}+1)}$,
∴m2≥$\frac{{{a}^{2}-a}^{4}}{8({a}^{2}+1)^{2}}$,令f(a)=$\frac{{{a}^{2}-a}^{4}}{8({a}^{2}+1)^{2}}$,a2+1=t,
則f(a)=$\frac{t-1-(t-1)^{2}}{8{t}^{2}}$=-$\frac{1}{4}$($\frac{1}{t}$-$\frac{3}{4}$)2+$\frac{1}{64}$.
∵0≤a≤1,∴1≤t≤2,∴$\frac{1}{2}$≤$\frac{1}{t}$≤1.
∴當$\frac{1}{t}=\frac{3}{4}$時,f(a)取得最大值$\frac{1}{64}$.即m2≥$\frac{1}{64}$.
∴m≥$\frac{1}{8}$,∴m的最小值為$\frac{1}{8}$.
點評 本題考查了橢圓的定義,兩點間的距離公式、二次函數的單調性、換元法、分類討論的思想方法是解題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
 我們通常把圓、橢圓、拋物線、雙曲線統稱為圓錐曲線.通過普通高中課程實驗教科書《數學》2-1第二章《圓錐曲線與方程》章頭引言我們知道,用一個垂直于圓錐的軸的平面截圓錐,截口曲線(截面與圓錐側面的交線)是一個圓.實際上,設圓錐母線與軸所成角為α,不過圓錐頂點的截面與軸所成角為θ.當θ=$\frac{π}{2}$,截口曲線為圓,當$α<θ<\frac{π}{2}$時,截口曲線為橢圓;當0≤θ<α時,截口曲線為雙曲線; 當θ=α時,截口曲線為拋物線;如圖2,正方體ABCD-A′B′C′D′中,M為BC邊的中點,點P在底面A′B′C′D′上運動并且使∠MAC′=∠PAC′,那么點P的軌跡是( )
我們通常把圓、橢圓、拋物線、雙曲線統稱為圓錐曲線.通過普通高中課程實驗教科書《數學》2-1第二章《圓錐曲線與方程》章頭引言我們知道,用一個垂直于圓錐的軸的平面截圓錐,截口曲線(截面與圓錐側面的交線)是一個圓.實際上,設圓錐母線與軸所成角為α,不過圓錐頂點的截面與軸所成角為θ.當θ=$\frac{π}{2}$,截口曲線為圓,當$α<θ<\frac{π}{2}$時,截口曲線為橢圓;當0≤θ<α時,截口曲線為雙曲線; 當θ=α時,截口曲線為拋物線;如圖2,正方體ABCD-A′B′C′D′中,M為BC邊的中點,點P在底面A′B′C′D′上運動并且使∠MAC′=∠PAC′,那么點P的軌跡是( )| A. | 一段雙曲線弧 | B. | 一段橢圓弧 | C. | 一段圓弧 | D. | 一段拋物線弧 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,三棱錐的四個頂點P、A、B、C在同一個球面上,頂點P在平面ABC內的射影是H,若球心在直線PH上,則點H一定是△ABC的( )
如圖,三棱錐的四個頂點P、A、B、C在同一個球面上,頂點P在平面ABC內的射影是H,若球心在直線PH上,則點H一定是△ABC的( )| A. | 重心 | B. | 垂心 | C. | 內心 | D. | 外心 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
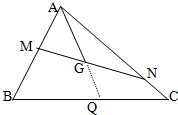 如圖所示,已知點G是△ABC的重心,過點G作直線與AB,AC兩邊分別交于M,N兩點,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,則x+y的最小值為( )
如圖所示,已知點G是△ABC的重心,過點G作直線與AB,AC兩邊分別交于M,N兩點,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,則x+y的最小值為( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 15 | B. | 12 | C. | 9 | D. | 與k的取值有關 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com