
| A. | 若?n∈N*總有cn⊥bn成立,則數列{an}是等比數列 | |
| B. | 若?n∈N*總有cn∥bn成立成立,則數列{an}是等比數列 | |
| C. | 若?n∈N*總有cn⊥bn成立,則數列{an}是等差數列 | |
| D. | 若?n∈N*總有cn∥bn成立,則數列{an}是等差數列 |
分析 根據題意,分析平面向量平行、垂直的坐標表示,判斷數列{an}是否為等差或等比數列.
解答 解:若cn∥bn成立,則-2nan=(2n+2)an+1,即-nan=(n+1)an+1,即$\frac{{a}_{n+1}}{{a}_{n}}$=-$\frac{n}{n+1}$,
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$…$\frac{{a}_{2}}{{a}_{1}}$•a1=(-$\frac{n-1}{n}$)•(-$\frac{n-2}{n-1}$)•…•(-$\frac{1}{2}$)•a1=$\frac{1}{n}$(-1)n-1a1,
∴數列{an}既不是等差數列,也不是等比數列,
∴B,D錯誤,
若?n∈N*總有cn⊥bn成立,則(2n+2)an-2nan+1=0,nan=(n+1)an+1,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$…$\frac{{a}_{2}}{{a}_{1}}$•a1=$\frac{n}{n-1}$•$\frac{n-1}{n-2}$•…•2•a1=na1,
∴數列{an}是等差數列,
∴A錯誤,C正確,
故選:C
點評 本題考查了平面向量平行的坐標表示,也考查了等差與等比數列的應用問題,中檔題目.


科目:高中數學 來源: 題型:選擇題

| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
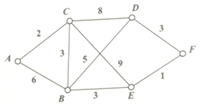 某市A,B,C,D,E,F六個城區欲架設光纜,如圖所示,兩點之間的線段及線段上的相應數字分別對應城區可以架設光纜及所需光纜的長度,如果任意兩個城市之間均勻光纜相通,則所需光纜的總長度的最小值是( )
某市A,B,C,D,E,F六個城區欲架設光纜,如圖所示,兩點之間的線段及線段上的相應數字分別對應城區可以架設光纜及所需光纜的長度,如果任意兩個城市之間均勻光纜相通,則所需光纜的總長度的最小值是( )| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,2] | B. | (-∞,2) | C. | [3,+∞) | D. | $(-∞,\frac{5}{2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 消費金額 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 女性人數 | 5 | 10 | 15 | 47 | x |
| 男性人數 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 總計 | |
| 網購達人 | |||
| 非網購達人 | |||
| 總計 |
| P(Χ2>k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com