
分析 由題意,當D在BC的正上方時S△DBC面積最大,A為BC的正下方時S△ABC面積最大,設BC為2x,可求DH=$\sqrt{1-{x}^{2}}$,S四邊形ABCD=x2+x$\sqrt{1-{x}^{2}}$,設x=sinθ,則利用三角函數恒等變換的應用化簡可得S四邊形=$\frac{1}{2}$[1+$\sqrt{2}$sin(2θ-$\frac{π}{4}$)],利用正弦函數的性質即可求得S四邊形的最大值.
解答 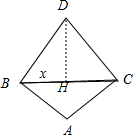 解:∵∠BAC=90°,BD+CD=2,
解:∵∠BAC=90°,BD+CD=2,
∴D在以BC為焦點的橢圓上運動,A在以BC為直徑的圓上運動,
∴當D在BC的正上方時S△DBC面積最大,A為BC的正下方時S△ABC面積最大,此時,設BC為2x,則DH=$\sqrt{1-{x}^{2}}$,
∴S四邊形ABCD=S△BCD+SABC=x$•\sqrt{1-{x}^{2}}$+$\frac{1}{2}•2x•x$=x2+x$\sqrt{1-{x}^{2}}$,
設x=sinθ,則$\sqrt{1-{x}^{2}}$=cosθ,
∴S四邊形=sin2θ+sinθcosθ=$\frac{1}{2}$(2sin2θ+2sinθcosθ)=$\frac{1}{2}$(1-cos2θ+sin2θ)=$\frac{1}{2}$[1+$\sqrt{2}$sin(2θ-$\frac{π}{4}$)],
∴當sin(2θ-$\frac{π}{4}$)=1時,即θ=$\frac{3π}{8}$時,S四邊形取得最大值,最大值為:$\frac{1+\sqrt{2}}{2}$.
故答案為:$\frac{1+\sqrt{2}}{2}$.
點評 本題主要考查了圓和橢圓的性質,考查了三角函數恒等變換的應用以及正弦函數的性質的綜合應用,考查了運動思想,轉化思想和數形結合思想,屬于中檔題.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
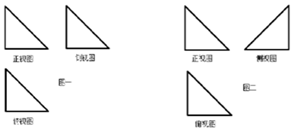 小明在解決三視圖還原問題時,錯把圖一的三視圖看成圖二的三視圖,假設圖一所對應幾何體中最大的面積為S1,圖二所對應幾何體中最大面的面積為S2,三視圖中所有三角形均為全等的等腰直角三角形,則$\frac{{S}_{1}}{{S}_{2}}$=( )
小明在解決三視圖還原問題時,錯把圖一的三視圖看成圖二的三視圖,假設圖一所對應幾何體中最大的面積為S1,圖二所對應幾何體中最大面的面積為S2,三視圖中所有三角形均為全等的等腰直角三角形,則$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | 1 | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com