
分析 利用兩個(gè)向量共線(xiàn)的性質(zhì)可得$\overrightarrow a$與$\overrightarrow b$的夾角π,設(shè)$\overrightarrow{b}$=-λ•$\overrightarrow{a}$,λ>0,根據(jù)$|{\overrightarrow b}|=3\sqrt{5}$,求得λ的值,可得$\overrightarrow b$的坐標(biāo).
解答 解:∵平面向量$\overrightarrow a=(-1,2)$,$|{\overrightarrow b}|=3\sqrt{5}$,設(shè)$\overrightarrow a$與$\overrightarrow b$的夾角為θ,且cosθ=-1,
∴$\overrightarrow a$與$\overrightarrow b$的夾角θ=π,設(shè)$\overrightarrow{b}$=-λ•$\overrightarrow{a}$=(λ,-2λ),λ>0,
∴λ2+(-2λ)2=${(3\sqrt{5})}^{2}$,∴λ=3,∴$\overrightarrow b$的坐標(biāo)為(3,-6),
故答案為:(3,-6).
點(diǎn)評(píng) 本題主要考查兩個(gè)向量共線(xiàn)的性質(zhì),求向量的模,屬于基礎(chǔ)題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
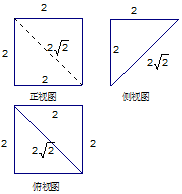
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com