
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
分析 設f(x)=x2-xlnx+2,判斷f(x)的單調性,求出y=k(x+2)與f(x)相切和過點($\frac{1}{2}$,f($\frac{1}{2}$))時的斜率,即可得出k的范圍.
解答 解:令f(x)=x2-xlnx+2,則f′(x)=2x-lnx-1,
f″(x)=2-$\frac{1}{x}$,
∵x$≥\frac{1}{2}$,∴f″(x)≥0,
∴f′(x)在[$\frac{1}{2}$,+∞)上單調遞增,
∴f′(x)≥f($\frac{1}{2}$)=-ln$\frac{1}{2}$=ln2>0,
∴f(x)在[$\frac{1}{2}$,+∞)上單調遞增,
作出y=f(x)與y=k(x+2)的函數圖象如圖所示: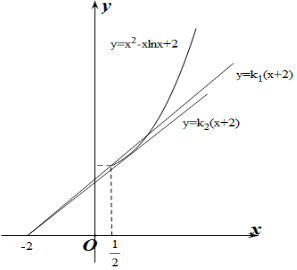
設y=k1(x+2)經過點($\frac{1}{2}$,f($\frac{1}{2}$)),又f($\frac{1}{2}$)=$\frac{9}{4}$-$\frac{1}{2}$ln$\frac{1}{2}$=$\frac{9}{4}+\frac{1}{2}ln2$,
∴k1=$\frac{\frac{9}{4}+\frac{1}{2}ln2}{\frac{1}{2}+2}$=$\frac{9}{10}+\frac{ln2}{5}$,
設y=k2(x+2)與f(x)的圖象相切,切點為(x0,y0),
則$\left\{\begin{array}{l}{{y}_{0}={k}_{2}({x}_{0}+2)}\\{{y}_{0}={{x}_{0}}^{2}-{x}_{0}ln{x}_{0}+2}\\{2{x}_{0}-ln{x}_{0}-1={k}_{2}}\end{array}\right.$,解得x0=1,y0=3,k2=1,
∵關于x的方程x2-xlnx+2=k(x+2)在[$\frac{1}{2}$,+∞)上有兩解,
∴y=f(x)與y=k(x+2)有兩個交點,
∴1<k≤$\frac{9}{10}+\frac{ln2}{5}$.
故選A.
點評 本題考查了函數零點個數與函數圖象的關系,函數單調性的判斷,屬于中檔題.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案科目:高中數學 來源: 題型:選擇題
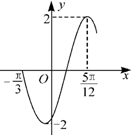
| A. | $2\;,\;\frac{2π}{3}$ | B. | $2\;,\;-\frac{π}{3}$ | C. | $1\;,\;\frac{π}{12}$ | D. | $1\;,\;-\frac{π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
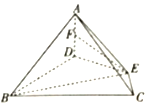 如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com