
分析 本題考查的知識點是類比推理,由圓的性質類比猜想橢圓的類似性質,一般的思路是:點到點,線到線,直徑到直徑等類比后的結論應該為關于橢圓的一個類似結論.
解答 解:定理:如果圓x2+y2=r2(r>0)上異于一條直徑兩個端點的任意一點與這條直徑兩個端點連線的都斜率存在,
則這兩條直線的斜率乘積為定值-1,即kABkOM=-1.
運用類比推理,寫出該定理在橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中的推廣:
若AB是圓錐曲線的一條不經過點O且不垂直于坐標軸的弦,M是弦AB的中點,則kABkOM=-$\frac{{b}^{2}}{{a}^{2}}$.
故答案為:若AB是圓錐曲線的一條不經過點O且不垂直于坐標軸的弦,M是弦AB的中點,則${K_{AB}}•{K_{OM}}=-\frac{b^2}{a^2}$.
點評 類比推理的一般步驟是:(1)找出兩類事物之間的相似性或一致性;(2)用一類事物的性質去推測另一類事物的性質,得出一個明確的命題(猜想).


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
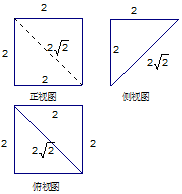
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ex2-ex1>lnx2-lnx1 | B. | ex2-ex1<lnx2-lnx1 | ||
| C. | x2ex1>x1ex2 | D. | x2ex1<x1ex2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com