
| A. | a2<b2 | B. | $\sqrt{-a}<\sqrt{b}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | $\frac{a}{b}$+$\frac{b}{a}$≥2 |
分析 根據題意,依次分析選項,對于A、B,舉出反例可得其錯誤,對于C,分析可得$\frac{1}{a}$<0而$\frac{1}{b}$>0,易得C正確,對于D,分析a、b的符號可得$\frac{a}{b}$<0且$\frac{b}{a}$<0,則有$\frac{a}{b}$+$\frac{b}{a}$<0,可得D錯誤;綜合即可得答案.
解答 解:根據題意,依次分析選項:
對于A、若a=-3,而b=1,則a2>b2.故A錯誤;
對于B、若a=-9,而b=1,則有$\sqrt{-(-9)}$>$\sqrt{a}$,故B錯誤;
對于C,若a<0,則$\frac{1}{a}$<0,而b>0,則$\frac{1}{b}$>0,故$\frac{1}{a}$<$\frac{1}{b}$,故C正確;
對于D,若a<0,b>0,故$\frac{a}{b}$<0,$\frac{b}{a}$<0,則有$\frac{a}{b}$+$\frac{b}{a}$<0,故D錯誤;
故選C.
點評 本題考查不等式的性質,關鍵是熟悉不等式的性質,對于不成立的不等式,可以舉出反例,進行判斷.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
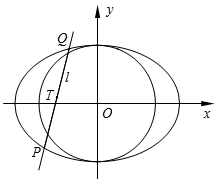 在平面直角坐標系xOy中,已知圓O:x2+y2=b2經過橢圓$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦點.
在平面直角坐標系xOy中,已知圓O:x2+y2=b2經過橢圓$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com