
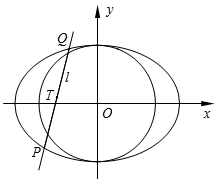
 在平面直角坐標系xOy中,已知圓O:x2+y2=b2經過橢圓$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦點.
在平面直角坐標系xOy中,已知圓O:x2+y2=b2經過橢圓$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦點.分析 (1)橢圓E的焦點在x軸上,圓O:x2+y2=b2經過橢圓E的焦點,所以橢圓的半焦距c=b,所以2b2=4,即b2=2,即可求出橢圓E的方程;
(2)求出T的坐標,利用斜率公式,結合條件,即可求k1•k2的值.
解答 解:(1)因0<b<2,所以橢圓E的焦點在x軸上,
又圓O:x2+y2=b2經過橢圓E的焦點,所以橢圓的半焦距c=b,…(3分)
所以2b2=4,即b2=2,所以橢圓E的方程為$\frac{x^2}{4}+\frac{y^2}{2}=1$.…(6分)
(2)設P(x1,y1),Q(x2,y2),T(x0,y0),
聯立$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{2}=1\\ y=kx+m\end{array}\right.$,消去y,得(1+2k2)x2+4kmx+2m2-4=0,
所以${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}$,又2m2-2k2=1,所以x1+x2=$-\frac{2k}{m}$,
所以${x_0}=-\frac{k}{m}$,${y_0}=m-k•\frac{k}{m}=\frac{1}{2m}$,…(10分)
則${k_1}•{k_2}=\frac{{\frac{1}{2m}}}{{-\frac{k}{m}+1}}•\frac{{\frac{1}{2m}}}{{-\frac{k}{m}-1}}=\frac{1}{{4{k^2}-4{m^2}}}=\frac{1}{{-2(2{m^2}-2{k^2})}}=-\frac{1}{2}$.…(14分)
點評 本題考查橢圓的方程與性質,考查直線與橢圓的位置關系,考查韋達定理的運用,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | a2<b2 | B. | $\sqrt{-a}<\sqrt{b}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | $\frac{a}{b}$+$\frac{b}{a}$≥2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 相交 | B. | 相切 | C. | 相離 | D. | 以上均有可能 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,2) | B. | (2,+∞) | C. | $(1,\;\sqrt{2})$ | D. | $(\sqrt{2},\;+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 120 | B. | 40 | C. | 30 | D. | 20 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
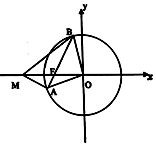 已知圓O:x2+y2=16及圓內一點F(-3,0),過F任作一條弦AB.
已知圓O:x2+y2=16及圓內一點F(-3,0),過F任作一條弦AB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com