
分析 (I)根據切線方程與直線y=2x平行得到切線的斜率為2,即可得到f'(e)=2,求出函數的導函數把f'(e)=2代入即可求出a的值得到函數的解析式;
(Ⅱ)由(Ⅰ)求得f'(x),令f'(x)=0可得極值點$\frac{1}{e}$,按照極值點與區間位置關系分類討論:當0<t<$\frac{1}{e}$<t+2時,當$\frac{1}{e}$≤t<t+2時可求得最值;
(Ⅲ)k=$\frac{f′({x}_{2})-f′({x}_{1})}{{x}_{2}-{x}_{1}}$=$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}$,要證x1<$\frac{1}{k}$<x2,即證x1<$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}$<x2,等價于1<$\frac{\frac{{x}_{2}}{{x}_{1}}-1}{ln\frac{{x}_{2}}{{x}_{1}}}$<$\frac{{x}_{2}}{{x}_{1}}$,令t=$\frac{{x}_{2}}{{x}_{1}}$,則只證1<$\frac{t-1}{lnt}$<t,由t>1,知lnt>0,故等價于證明lnt<t-1<tlnt,構造函數利用導數可證明兩不等式;
解答 解:(I)由點(e,f(e))處的切線方程與直線2x-y=0平行,
得該切線斜率為2,即f′(e)=2.
又∵f′(x)=a(lnx+1),令a(lne+1)=2,解得a=1,
∴f(x)=xlnx.
(II)由(I)知f′(x)=lnx+1,
顯然f′(x)=0時x=e-1,當x∈(0,$\frac{1}{e}$)時,f′(x)<0,
∴函數f(x)在(0,$\frac{1}{e}$)上單調遞減.
當x∈($\frac{1}{e}$,+∞)時,f′(x)>0,
∴函數f(x)在($\frac{1}{e}$,+∞)上單調遞增,
①0<t<$\frac{1}{e}$<t+2,即0<t<$\frac{1}{e}$時,f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$;
②$\frac{1}{e}$≤t<t+2,即t≥$\frac{1}{e}$時,f(x)在[t,t+2]上單調遞增,f(x)min=f(t)=tlnt;
∴f(x)min=$\left\{\begin{array}{l}{-\frac{1}{e},}&{0<t<\frac{1}{e}}\\{tlnt,}&{t≥\frac{1}{e}}\end{array}\right.$;
(Ⅲ)k=$\frac{f′({x}_{2})-f′({x}_{1})}{{x}_{2}-{x}_{1}}$=$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}$,
要證x1<$\frac{1}{k}$<x2,即證x1<$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}$<x2,等價于1<$\frac{\frac{{x}_{2}}{{x}_{1}}-1}{ln\frac{{x}_{2}}{{x}_{1}}}$<$\frac{{x}_{2}}{{x}_{1}}$,
令t=$\frac{{x}_{2}}{{x}_{1}}$,則只證1<$\frac{t-1}{lnt}$<t,由t>1,知lnt>0,故等價于證明lnt<t-1<tlnt,…12分
①設g(t)=t-1-lnt(t≥1),則g'(t)=1-$\frac{1}{t}$≥0,(t≥1),故g(t)在[1,+∞)上遞增,
∴t>1時,g(t)=t-1-lnt>g(1)=0,即t-1>lnt,(t>1);
②設h(t)=tlnt-t+1(t≥1),則h'(t)=lnt≥0,(t≥1),故h(t)在[1,+∞)上是增函數,
∴當t>1時,h(t)=tlnt-t+1>h(1)=0,即tlnt>t-1;
由①②可知,lnt<t-1<tlnt成立,故x1<$\frac{1}{k}$<x2…14分
點評 本題考查導數的幾何意義、利用導數研究函數的最值及不等式的證明等知識,考查分類討論思想、函數思想,考查學生綜合運用知識分析問題解決問題的能力、推理論證能力,該題綜合性強,能力要求較高.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
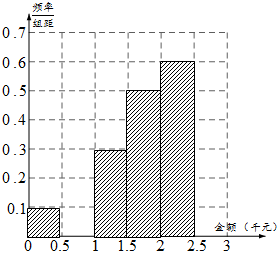 某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):
某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):| 網購金額 (單位千元) | 頻數 | 頻率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合計 | 60 | 1.00 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
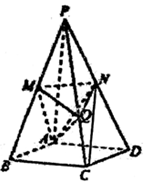 如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分別為PB,PD的中點.
如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分別為PB,PD的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com