
| 參加紀念活動的環節數 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
分析 (1)由題意可知:$m+n+\frac{1}{6}+\frac{1}{3}=1$,再由m=2n,能求出這60名抗戰老兵中參加紀念活動的環節數為0,1,2,3的抗戰老兵的人數分別為10,20,10,20,由此利用分層抽樣法能求出參加紀念活動的環節數為1的抗戰老兵中應抽取的人數.
(2)抽取的這6名抗戰老兵中1名參加了0個環節,記為A,2名參加了1個環節,記為B,C,1名參加了2個環節,分別記為D,2名參加了3個環節,分別記為E,F,從這6名抗戰老兵中隨機抽取2人,利用列舉法能求出這2名抗戰老兵中至少有1人參加紀念活動的環節數為3的概率.
解答 解:(1)由題意可知:$m+n+\frac{1}{6}+\frac{1}{3}=1$,
又m=2n,解得$m=\frac{1}{3}$,$n=\frac{1}{6}$
故這60名抗戰老兵中參加紀念活動的環節數為0,1,2,3的抗戰老兵的人數分別為10,20,10,20,
其中參加紀念活動的環節數為1的抗戰老兵中應抽取的人數為$20×\frac{6}{60}=2$.
(2)由(1)可知抽取的這6名抗戰老兵中1名參加了0個環節,記為A,
2名參加了1個環節,記為B,C,1名參加了2個環節,分別記為D,
2名參加了3個環節,分別記為E,F,
從這6名抗戰老兵中隨機抽取2人,有:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),
共15個基本事件,
記“這2名抗戰老兵中至少有1人參加紀念活動的環節數為3”位事件M,
則事件M包含的基本事件為:
(A,E),(A,F),(B,E),(B,F),(C,E),(C,F),
(D,E),(D,F),(E,F),共9個基本事件.
所以這2名抗戰老兵中至少有1人參加紀念活動的環節數為3的概率$P(M)=\frac{9}{15}=\frac{3}{5}$.
點評 本題分層抽樣的應用,考查概率的求法,考查推理論證能力、運算求解能力、數據處理能力,考查化歸與轉化思想、數形結合思想,是基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
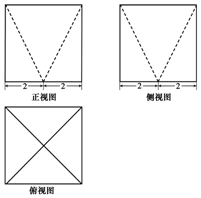 某幾何體的三視圖如圖所示,圖中的四邊形都是邊長為4的正方形,兩條虛線互相垂直,則該幾何體的表面積是( )
某幾何體的三視圖如圖所示,圖中的四邊形都是邊長為4的正方形,兩條虛線互相垂直,則該幾何體的表面積是( )| A. | $96+16\sqrt{5}$ | B. | $80+16\sqrt{5}$ | C. | $80+32\sqrt{5}$ | D. | $96+32\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
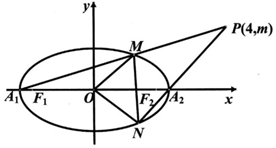 如圖,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O為坐標原點.
如圖,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O為坐標原點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-1,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{3}{4}$] | B. | (0,1] | C. | [$\frac{3}{4}$,1] | D. | [$\frac{3}{2}$,1] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com