
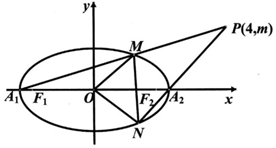
 如圖,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O為坐標原點.
如圖,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O為坐標原點.分析 (Ⅰ)由離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,列式計算a,b,即可得橢圓C的方程的方程
(Ⅱ)直線PA1,PA1的方程分別為:y=$\frac{m}{6}(x+2)$,y=$\frac{m}{2}(x-2)$,由$\left\{\begin{array}{l}{y=\frac{m}{6}(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(9+m2)x2+4m2x+4m2-36=0,可得${x}_{M}=\frac{18-2{m}^{2}}{9+{m}^{2}}$,${y}_{M}=\frac{m}{6}({x}_{M}+2)$=$\frac{6m}{9+{m}^{2}}$,同理可得xN=$\frac{2{m}^{2}-2}{1+{m}^{2}}$,${y}_{N}=\frac{m}{2}({x}_{N}-2)$=$\frac{-2m}{1+{m}^{2}}$,直線MN的方程為:$y-\frac{-2m}{1+{m}^{2}}=\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})$,y=$\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})-\frac{2m}{1+{m}^{2}}$=$\frac{2m}{3-{m}^{2}}$$(x-\frac{2{m}^{2}-2}{1+{m}^{2}}-\frac{3-{m}^{2}}{1+{m}^{2}})$=$\frac{2m}{3-{m}^{2}}(x-1)$,可得直線MN過定點(1,0),故設MN的方程為:x=ty+1,
由$\left\{\begin{array}{l}{x=ty+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(t2+4)y2+2ty-3=0,|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{{t}^{2}+3}}{{t}^{2}+4}$,即△OMN的面積S=$\frac{1}{2}×1×$(y1-y2)=2$\frac{\sqrt{{t}^{2}+3}}{{t}^{2}+4}$利用函數單調性即可求出面積最大值.
解答 解:(Ⅰ)∵離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2c=2\sqrt{3}}\end{array}\right.$,∴a=2,c=$\sqrt{3}$,則b=1
∴橢圓C的方程的方程為:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)由(Ⅰ)得A1(-2,0),A2(2,0),
直線PA1,PA1的方程分別為:y=$\frac{m}{6}(x+2)$,y=$\frac{m}{2}(x-2)$
由$\left\{\begin{array}{l}{y=\frac{m}{6}(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(9+m2)x2+4m2x+4m2-36=0
∴-2+xM=$\frac{-4{m}^{2}}{9+{m}^{2}}$,可得.${x}_{M}=\frac{18-2{m}^{2}}{9+{m}^{2}}$,${y}_{M}=\frac{m}{6}({x}_{M}+2)$=$\frac{6m}{9+{m}^{2}}$
由$\left\{\begin{array}{l}{y=\frac{m}{2}(x-2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得(1+m2)x2-4mx+4m2-4=0
∴2+xN=$\frac{4{m}^{2}}{1+{m}^{2}}$,可得xN=$\frac{2{m}^{2}-2}{1+{m}^{2}}$,${y}_{N}=\frac{m}{2}({x}_{N}-2)$=$\frac{-2m}{1+{m}^{2}}$
${k}_{MN}=\frac{{y}_{M}-{y}_{N}}{{x}_{M}-{x}_{N}}=\frac{2m}{3-{m}^{2}}$,
直線MN的方程為:$y-\frac{-2m}{1+{m}^{2}}=\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})$,
y=$\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})-\frac{2m}{1+{m}^{2}}$=$\frac{2m}{3-{m}^{2}}$$(x-\frac{2{m}^{2}-2}{1+{m}^{2}}-\frac{3-{m}^{2}}{1+{m}^{2}})$=$\frac{2m}{3-{m}^{2}}(x-1)$
可得直線MN過定點(1,0),故設MN的方程為:x=ty+1
由$\left\{\begin{array}{l}{x=ty+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(t2+4)y2+2ty-3=0
設M(x1,y1),N(x2,y2),則${y}_{1}+{y}_{2}=\frac{-2t}{{t}^{2}+4}$,${y}_{1}{y}_{2}=\frac{-3}{{t}^{2}+4}$
|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{{t}^{2}+3}}{{t}^{2}+4}$
∴△OMN的面積S=$\frac{1}{2}×1×$(y1-y2)=2$\frac{\sqrt{{t}^{2}+3}}{{t}^{2}+4}$
令$\sqrt{{t}^{2}+3}=d,(d≥\sqrt{3})$,則s=$\frac{2d}{p9vv5xb5^{2}+1}=\frac{2}{d+\frac{1}p9vv5xb5}$
∵$d≥\sqrt{3}$,且函數f(d)=d+$\frac{1}p9vv5xb5$在[$\sqrt{3}$,+∞)遞增,
∴當d=$\sqrt{3}$,s取得最小值$\frac{\sqrt{3}}{2}$
點評 本題考查了橢圓的方程,直線與橢圓的位置關系,方程思想,轉化思想,考查了運算能力,屬于難題


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 參加紀念活動的環節數 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2015 | B. | -2017 | C. | -2015 | D. | -2016 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com