
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 19種 | B. | 38種 | C. | 120種 | D. | 240種 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
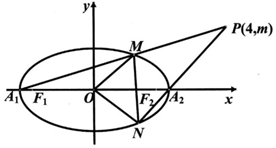 如圖,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O為坐標原點.
如圖,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O為坐標原點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-1,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-2≤x<0或3<x≤4} | B. | {x|-2≤x≤0或3≤x≤4} | C. | {x|-2<x≤4} | D. | {x|0<x<3} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com