
分析 設切點為(x0,y0),根據導數的幾何意義求出曲線在點x0處的切線斜率,可得切線方程,代入切點,便可建立關于x0的方程.求得x0,從而求得過點且與曲線C相切的直線方程.
解答 解:設直線與曲線切于點(x0,y0)(x0≠0),∵y=$\frac{1}{3}$x3-x,
∴y′=x02-1.
∴切線方程為y+2=(x02-1)(x-2)
∴y0+2=(x02-1)(x0-2)
∵y0=$\frac{1}{3}$x03-x0,
∴$\frac{1}{3}$x03-x0+2=(x02-1)(x0-2)
∴x0=0,或x02=3,∴k=x02-1=8或-1,
故直線l的方程y=-x或y=8x-18.
故答案為:y=-x或y=8x-18.
點評 此題考查學生會利用導數求曲線上過某點切線方程的斜率,會根據一點坐標和斜率寫出直線的方程,是一道綜合題.


科目:高中數學 來源: 題型:解答題
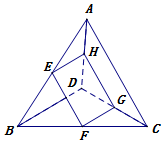 如圖,E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA上的中點.
如圖,E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA上的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{8i}{5}$ | B. | $\frac{8i}{5}$ | C. | $-\frac{6}{5}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p是q的充分不必要條件 | B. | p是q的必要不充分條件 | ||
| C. | p是q的既不充分也不必要條件 | D. | p是q的充要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $f({-\frac{3}{2}})>f({{a^2}+2a+\frac{5}{2}})$ | B. | $f({-\frac{3}{2}})<f({{a^2}+2a+\frac{5}{2}})$ | C. | $f({-\frac{3}{2}})≥f({{a^2}+2a+\frac{5}{2}})$ | D. | $f({-\frac{3}{2}})≤f({{a^2}+2a+\frac{5}{2}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 看營養說明 | 不看營養說明 | 合計 | |
| 男大學生 | 26 | 6 | 32 |
| 女大學生 | 14 | 18 | 32 |
| 合計 | 40 | 24 | 64 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com